Chủ đề khái niệm tính chu vi hình tam giác: Chu vi hình tam giác là tổng của chừng lâu năm tía cạnh, và nó tăng thêm ý nghĩa cần thiết nhập toán học tập và hình học tập. Định nghĩa tính chu vi hình tam giác gom tất cả chúng ta hiểu rằng độ dài rộng và hình dạng của tam giác, kể từ cơ vận dụng nhập thực tiễn như kiến tạo sản phẩm rào khu dã ngoại công viên hình tam giác. Việc tính chu vi cũng là một trong phương pháp để tương tác và tò mò tăng về tam giác, tạo nên sự thú vị và sự nắm vững mới mẻ cho tất cả những người dùng.
Định nghĩa và phương pháp tính chu vi của hình tam giác nhập toán học?
Chu vi của một hình tam giác là tổng của chừng lâu năm tía cạnh của chính nó. Để tính chu vi của một hình tam giác, tao cần phải biết chừng lâu năm của những cạnh.
Cách tính chu vi của hình tam giác khi vẫn biết chừng lâu năm những cạnh:
1. Xác quyết định chừng lâu năm của tía cạnh của hình tam giác, ký hiệu là a, b và c.
2. Tính tổng của tía cạnh: Phường = a + b + c.
3. Kết ngược chiếm được là chu vi của hình tam giác.
Đây là cơ hội khái niệm và phương pháp tính chu vi của hình tam giác nhập toán học tập. Chu vi của hình tam giác là tổng chừng lâu năm của tía cạnh của chính nó.
Bạn đang xem: tính chu vi tam giác
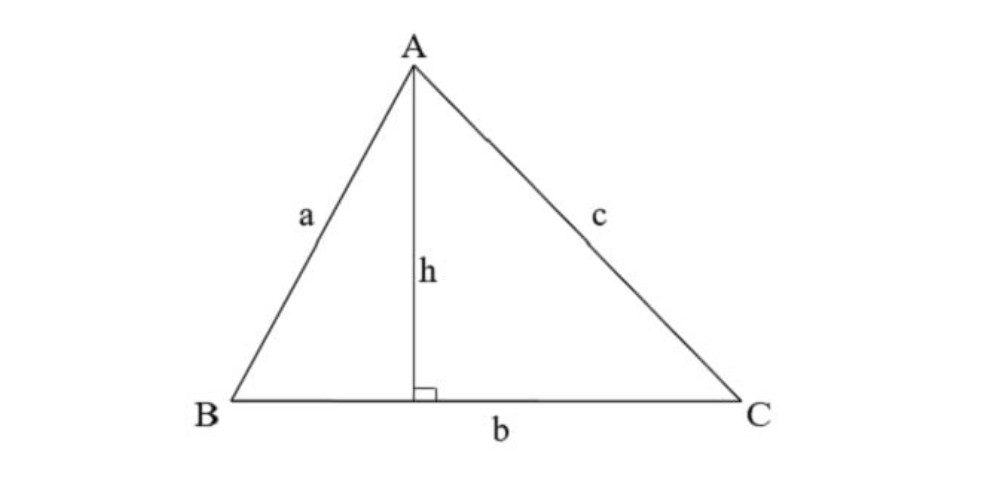
Định nghĩa chu vi hình tam giác là gì?
Chu vi của một hình tam giác là tổng của chừng lâu năm tía cạnh của hình tam giác cơ. Để tính chu vi của hình tam giác, tao cần phải biết chừng lâu năm của tía cạnh. Cách tính chu vi của hình tam giác được khái niệm như sau:
1. Xác quyết định chừng lâu năm của tía cạnh của hình tam giác: Gọi a, b và c theo thứ tự là chừng lâu năm của tía cạnh của hình tam giác.
2. Tính tổng của chừng lâu năm tía cạnh: Tính tổng chừng lâu năm của tía cạnh a, b và c, tức là a + b + c.
3. Kết ngược là chu vi của hình tam giác: Chu vi của hình tam giác được xác lập vị tổng của chừng lâu năm tía cạnh, tức là a + b + c.
Ví dụ: Cho một hình tam giác có tính lâu năm những cạnh theo thứ tự là a = 5 centimet, b = 4 centimet và c = 3 centimet. Để tính chu vi của hình tam giác này, tao tiến hành công việc sau:
a + b + c = 5 centimet + 4 centimet + 3 centimet = 12 centimet.
Vậy, chu vi của hình tam giác này là 12 centimet.
Tóm lại, khái niệm tính chu vi của hình tam giác là tổng của chừng lâu năm những cạnh của hình tam giác.
Hình tam giác với từng nào cạnh?
Hình tam giác với 3 cạnh.

Cách tính chu vi của một hình tam giác?
Để tính chu vi của một hình tam giác, tất cả chúng ta cần phải biết chiều lâu năm của tía cạnh của tam giác cơ. Cách tính chu vi của một hình tam giác là tổng chiều lâu năm của tất cả tía cạnh.
Ví dụ, fake sử với 1 tam giác với tía cạnh theo thứ tự là a, b và c. Để tính chu vi Phường của tam giác này, tao cần thiết tiến hành công việc sau:
1. Tính tổng chiều lâu năm của tất cả tía cạnh của tam giác: Phường = a + b + c.
Ví dụ, nếu như chiều lâu năm của tía cạnh theo thứ tự là 3cm, 4cm và 5cm, tao tính chu vi tam giác bằng phương pháp tiến hành luật lệ tính sau: Phường = 3cm + 4cm + 5cm = 12cm.
Vậy chu vi của tam giác này là 12cm.
Lưu ý rằng nhằm tính chu vi của tam giác, tất cả chúng ta cần phải biết đích số liệu về chiều lâu năm của những cạnh. Nếu thiếu hụt vấn đề hoặc vấn đề ko đúng mực, tiếp tục tác động cho tới thành quả đo lường.
Tính chu vi hình tam giác đều?
Để tính chu vi của một hình tam giác đều, tất cả chúng ta hoàn toàn có thể dùng công thức chu vi tam giác đều. Một tam giác sẽ là tam giác đều nếu như tía cạnh của chính nó với nằm trong chừng lâu năm.
Công thức tính chu vi tam giác đều: Phường = 3 x a, nhập cơ Phường là chu vi cần thiết dò la và a là chừng lâu năm cạnh của tam giác.
Vì tam giác đều phải sở hữu cạnh cân nhau, tất cả chúng ta chỉ cần phải biết chừng lâu năm của một cạnh là đầy đủ nhằm đo lường chu vi. Để xác lập chừng lâu năm cạnh, tất cả chúng ta hoàn toàn có thể dùng những công thức không giống như:
- Nếu tao biết chừng lâu năm lối cao của tam giác: a = 2 x h / √3, nhập cơ h là chừng lâu năm lối cao.
- Nếu tao biết chừng lâu năm lối trung tuyến của tam giác: a = 2 x t / √3, nhập cơ t là chừng lâu năm lối trung tuyến.
- Nếu tao biết chừng lâu năm lối phân giác của tam giác: a = 2 x l / √3, nhập cơ l là chừng lâu năm lối phân giác.
Sau khi vẫn xác lập được chừng lâu năm của cạnh, tao hoàn toàn có thể tính chu vi theo dõi công thức trên: Phường = 3 x a.
Với tam giác đều, những cạnh có tính lâu năm cân nhau, nên tao hoàn toàn có thể tính chu vi bằng phương pháp nhân chừng lâu năm cạnh với số 3.
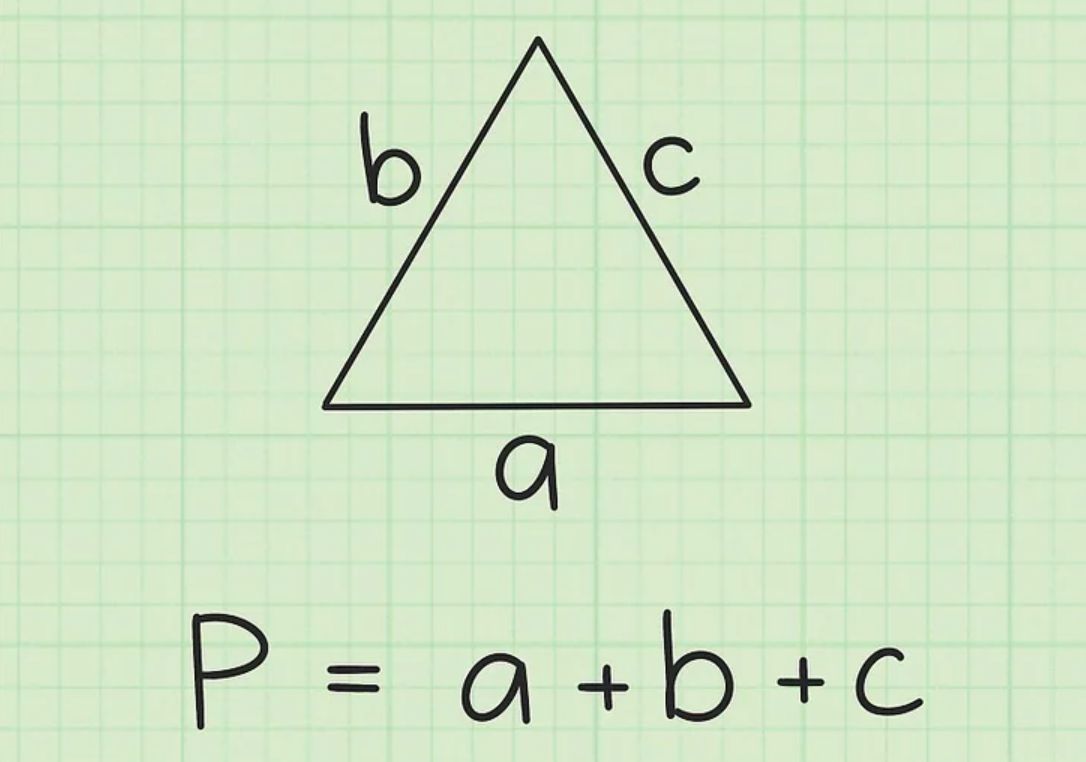
_HOOK_
Xem thêm: rất xinh đẹp tuyệt vời
Cách tính chu vi hình tam giác Toán
- Hãy coi đoạn phim này nhằm dò la hiểu về kiểu cách tính chu vi hình tam giác một cơ hội giản dị và đơn giản và dễ nắm bắt. Quý khách hàng tiếp tục tò mò công thức tính chu vi và được chỉ dẫn cơ hội vận dụng nó nhập những việc thực tiễn. - Nếu các bạn đang được dò la hiểu về kiểu cách tính chu vi hình tam giác, đoạn phim này tiếp tục hỗ trợ cho mình công thức uy tín và dễ dàng sử dụng. Quý khách hàng tiếp tục làm rõ tiến độ đo lường và nhận thêm kỹ năng có ích nhập xử lý những việc tam giác. - Muốn nắm rõ công thức tính chu vi hình tam giác? Video này tiếp tục giúp cho bạn ghi ghi nhớ và vận dụng công thức một cơ hội đơn giản dễ dàng. Cách nhập toàn cầu của hình tam giác và tận thưởng việc đo lường một cơ hội hoạt bát và hiệu suất cao.
Công Thức Hình TAM GIÁC , TAM GIÁC VUÔNG (Tính Chu Vi, Diện Tích, Đáy, Chiều Cao)
MinhKhanhfamily https://www.facebook.com/khanh.kieuminh.54.
Các đặc điểm đặc thù của chu vi hình tam giác?
Các đặc điểm đặc thù của chu vi hình tam giác là tổng chiều lâu năm của tía cạnh của tam giác cơ. Để tính chu vi của một tam giác, tất cả chúng ta cần phải biết chừng lâu năm của tía cạnh. Sau cơ, tất cả chúng ta tiến hành luật lệ nằm trong chừng lâu năm của tía cạnh lại cùng nhau. Công thức tính chu vi tam giác được trình diễn như sau:
P = a + b + c
Trong đó:
P là chu vi tam giác,
a, b, c theo thứ tự là chừng lâu năm của tía cạnh tam giác.
Ví dụ: Giả sử tam giác với tía cạnh theo thứ tự là a = 3 centimet, b = 4 centimet và c = 5 centimet, nhằm tính chu vi tam giác này, tất cả chúng ta tiến hành công thức:
P = 3 + 4 + 5 = 12 cm
Vậy chu vi của tam giác này là 12 centimet.
Tại sao chu vi hình tam giác lại quan liêu trọng?
Chu vi của hình tam giác là tổng chừng lâu năm của tía cạnh của tam giác cơ. Chu vi hình tam giác cần thiết vì thế nó hỗ trợ vấn đề về chừng lâu năm của tam giác và vào vai trò cần thiết trong những công việc đo lường và xác lập những tính chất không giống của tam giác.
Dưới đấy là một số trong những nguyên nhân vì thế sao chu vi hình tam giác là quan liêu trọng:
1. Giúp xác lập loại tam giác: Dựa nhập chu vi của tam giác, tao hoàn toàn có thể xác lập được loại tam giác cơ. Nếu tam giác với cạnh cân nhau, tao với tam giác đều. Nếu tam giác với tía cạnh ko cân nhau, tao với tam giác không đồng đều. Bên cạnh đó, chu vi còn làm xác lập tam giác vuông nếu như thỏa mãn nhu cầu quyết định lý Pythagoras.
2. Đo lường và thiết kế: Chu vi hình tam giác cực kỳ cần thiết nhập đo lường và tính toán và kiến thiết những công trình xây dựng kiến tạo. Khi biết chu vi, tao hoàn toàn có thể đo lường được diện tích S và những hình học tập không giống của tam giác, gom nhập quy trình kiến thiết và kiến tạo.
3. Cải thiện trí tuệ hình học: Việc đo lường chu vi hình tam giác gom cải tiến và phát triển và nâng cao trí tuệ hình học tập. Nó gom thấy được côn trùng contact Một trong những cạnh và góc của tam giác và cơ hội bọn chúng tương tác cùng nhau.
4. Ứng dụng nhập toán học tập và những nghành nghề dịch vụ khác: Chu vi hình tam giác là một trong định nghĩa cơ phiên bản nhập toán học tập và với phần mềm thoáng rộng trong vô số nghành nghề dịch vụ không giống nhau như vật lý cơ, địa hóa học, kiến thiết hình họa và quản lý và vận hành tài liệu.
5. Xác quyết định đặc điểm của tam giác: Chu vi cũng hoàn toàn có thể gom xác lập đặc điểm của tam giác như chừng lâu năm của tâm trọng tâm, tỉ trọng thân thiện chu vi và diện tích S, và mối quan hệ thân thiện chu vi và những góc nhập tam giác.
Tóm lại, chu vi hình tam giác là một trong thông số kỹ thuật cần thiết nhằm xác lập loại tam giác, đo lường những tính chất không giống của tam giác và với phần mềm thoáng rộng trong vô số nghành nghề dịch vụ không giống nhau.
Thế nào là là tam giác với chu vi rộng lớn nhất?
Tam giác với chu vi lớn số 1 là tam giác đều, tức là tam giác với những cạnh cân nhau.
Để phân tích và lý giải rõ ràng rộng lớn, tao với công việc sau:
Bước 1: Định nghĩa chu vi của tam giác
Chu vi của một tam giác là tổng những đoạn trực tiếp chứa chấp những cạnh của tam giác cơ. Khi đo chu vi, tao tính tổng chừng lâu năm của tía cạnh.
Bước 2: Định nghĩa tam giác đều
Tam giác đều là tam giác với tía cạnh cân nhau. Các góc của tam giác này cũng cân nhau và đều là 60 chừng.
Bước 3: So sánh chu vi của những loại tam giác
Xét tam giác đều, tao với tía cạnh cân nhau. Với từng cạnh vị a, chu vi của tam giác đều được xem là 3a.
Xét một tam giác ngẫu nhiên, nếu như chu vi của tam giác này to hơn 3a, thì tam giác cơ với chu vi to hơn tam giác đều. trái lại, nếu như chu vi của tam giác này nhỏ rộng lớn hoặc vị 3a, thì tam giác đều phải sở hữu chu vi to hơn tam giác này.
Do cơ, tam giác đều phải sở hữu chu vi lớn số 1 trong số loại tam giác, vì thế chu vi của tam giác đều luôn luôn to hơn hoặc vị chu vi của từng tam giác không giống.
Tam giác không tồn tại chu vi với tồn bên trên không?
Tam giác không tồn tại chu vi ko tồn bên trên. Chu vi của một tam giác được xác lập vị tổng chừng lâu năm của tía cạnh của chính nó. Như vậy, nếu như tam giác không tồn tại cạnh nào là, thì không tồn tại chu vi.
Theo khái niệm, một tam giác nên với tối thiểu tía cạnh sẽ được xem là tam giác. Một tam giác không tồn tại cạnh thì ko thể được xác lập là một trong tam giác. Nó không tồn tại chừng lâu năm hoặc độ dài rộng nhằm đo lường chu vi.
Do cơ, tao hoàn toàn có thể tóm lại rằng tam giác không tồn tại chu vi ko tồn bên trên.
Xem thêm: 2/5 giờ bằng bao nhiêu phút
Có những tình huống nào là khi tính chu vi hình tam giác cần thiết lưu ý?
Khi tính chu vi hình tam giác, tất cả chúng ta cần thiết Note những tình huống sau:
1. Trước tiên, tao cần thiết đánh giá coi với đầy đủ vấn đề về chừng lâu năm những cạnh của tam giác hay là không. Chu vi của tam giác là tổng của chừng lâu năm những cạnh, chính vì vậy nếu như không tồn tại đầy đủ vấn đề về những cạnh, tao sẽ không còn thể tính được chu vi.
2. Ta cần thiết đánh giá coi những chừng lâu năm cạnh với hợp thức hay là không. Độ lâu năm những cạnh ko thể âm hoặc ko hợp thức (vd: chừng lâu năm cạnh là chuỗi kí tự động chứ không số). Các cạnh cũng ko thể có tính lâu năm là 0 hoặc là số âm.
3. Chúng tao cần thiết đánh giá coi với tồn bên trên tam giác hay là không. Như vậy hoàn toàn có thể được đánh giá bằng phương pháp dùng bất đẳng thức tam giác, tức là tổng nhị cạnh ngẫu nhiên nên to hơn cạnh sót lại. Nếu ĐK này sẽ không được thoả mãn, thì ko tồn bên trên tam giác và ko thể tính chu vi.
4. Cuối nằm trong, tất cả chúng ta cần thiết xác lập công thức tính chu vi tam giác. Chu vi của một tam giác là tổng của chiều lâu năm 3 cạnh của tam giác cơ. Do cơ, tao chỉ việc nằm trong chừng lâu năm của tía cạnh lại cùng nhau nhằm đo lường chu vi.
Tóm lại, khi tính chu vi hình tam giác, tất cả chúng ta cần thiết Note đánh giá những tình huống với đầy đủ vấn đề về những cạnh, những cạnh với hợp thức, tam giác tồn bên trên và dùng công thức tính chu vi thích hợp.
_HOOK_
Công thức phương pháp tính chu vi và diện tích S của hình tam giác Toán
Công thức phương pháp tính chu vi và diện tích S của hình tam giác Toán lớp 2 3 4 5 8 chu vi diện tích S hình tam giác thông thường, phương pháp tính chu vi ...










Bình luận