tính chất đường trung trực

Đường trung trực của một quãng trực tiếp là đường thẳng liền mạch vuông góc với đoạn trực tiếp ấy bên trên trung điểm của chính nó vì thế lý thuyết cơ bạn dạng về hình học tập. Hãy kiểm tra công việc sau nhằm làm rõ rộng lớn về vì sao điều này đúng:
Bước 1: Định nghĩa lối trung trực: Đường trung trực của một quãng trực tiếp là đường thẳng liền mạch tuy nhiên hai tuyến đường trực tiếp này tách nhau ở góc cạnh vuông bên trên trung điểm của đoạn trực tiếp.
Bước 2: Định nghĩa trung điểm của đoạn thẳng: Trung điểm của một quãng trực tiếp đó là điểm nằm ở vị trí thân ái đoạn trực tiếp tê liệt, phân chia đoạn trực tiếp trở thành nhị đoạn trực tiếp đều bằng nhau.
Bước 3: Chứng minh rằng lối trung trực là lối thẳng: Để chứng tỏ điều này, tớ cần thiết chứng tỏ rằng lối trung trực thực hiện cho tới nhị đoạn trực tiếp tạo ra trở thành một góc vuông bên trên trung điểm của đoạn trực tiếp. Để thực hiện được điều này, tớ tiếp tục dùng những toan lý hình học tập cơ bạn dạng.
Định lý: Một đường thẳng liền mạch là lối trung trực của một quãng trực tiếp nếu như và chỉ nếu như nó vuông góc với đoạn trực tiếp này bên trên trung điểm của chính nó.
- Ta hiểu được trung điểm của đoạn trực tiếp phân chia đoạn trực tiếp trở thành nhị đoạn trực tiếp đều bằng nhau. Do tê liệt, tớ đem nhị tam giác nằm trong đem nhị cạnh đều bằng nhau và một góc đều bằng nhau. Như vậy suy đi ra tam giác nằm trong mang trong mình 1 góc vị 90 chừng.
- Vì lối trung trực là lối nối nhị điểm nằm ở vị trí nhị đầu của đoạn trực tiếp, nên nó tách đoạn trực tiếp tạo ra trở thành một góc vị 90 chừng bên trên trung điểm của đoạn trực tiếp. Đây đó là đặc thù cơ bạn dạng của lối trung trực.
Vậy nên, lối trung trực của một quãng trực tiếp là đường thẳng liền mạch vuông góc với đoạn trực tiếp này bên trên trung điểm của chính nó.

Lý thuyết lối trung trực là một trong định nghĩa nhập hình học tập, vận dụng so với đoạn trực tiếp. Đường trung trực của một quãng trực tiếp là đường thẳng liền mạch vuông góc với đoạn trực tiếp ấy bên trên trung điểm của chính nó.
Định nghĩa bên trên rất có thể hiểu một cơ hội đơn giản và giản dị như sau: Khi tớ mang trong mình 1 đoạn trực tiếp này tê liệt, thì lối trung trực của đoạn trực tiếp tê liệt là một trong đường thẳng liền mạch, với đặc thù là vuông góc với đoạn trực tiếp và trải qua trung điểm của chính nó.
Ví dụ, nếu như tớ đem đoạn trực tiếp AB, thì lối trung trực của đoạn trực tiếp này là đường thẳng liền mạch tuy nhiên vuông góc với AB bên trên trung điểm của AB. Đường trung trực này phân chia đoạn trực tiếp AB trở thành nhị phần đều bằng nhau, tức là kể từ điểm A cho tới lối trung trực và kể từ lối trung trực tới điểm B có tính nhiều năm đều bằng nhau.
Lý thuyết lối trung trực là một trong định nghĩa cần thiết nhập hình học tập và có tương đối nhiều phần mềm trong các việc giải những vấn đề tương quan cho tới đoạn trực tiếp và những tam giác.

Đường trung trực của một quãng trực tiếp là đường thẳng liền mạch nằm trong mặt mũi bằng chứa chấp đoạn trực tiếp tê liệt. Để xác lập lối trung trực, tớ cần thiết triển khai công việc sau đây:
Bước 1: Vẽ đoạn trực tiếp AB bên trên mặt mũi bằng.
Bước 2: Tìm điểm trung điểm M của đoạn trực tiếp AB. Điểm trung điểm là vấn đề nằm ở vị trí thân ái đoạn trực tiếp AB, đem nằm trong khoảng cách cho tới nhị đầu mút A và B của đoạn trực tiếp.
Bước 3: Vẽ một đường thẳng liền mạch d vuông góc với đoạn trực tiếp AB bên trên điểm M. Đường trực tiếp này gọi là lối trung trực của đoạn trực tiếp AB.
Khi vẽ lối trung trực, đường thẳng liền mạch d tiếp tục nằm trong mặt mũi bằng chứa chấp đoạn trực tiếp AB, ở trung tâm đoạn trực tiếp tê liệt và tạo ra trở thành góc vuông với đoạn trực tiếp AB bên trên điểm M.

Để xác lập lối trung trực của một quãng trực tiếp, tớ triển khai công việc sau đây:
1. Vẽ đoạn trực tiếp AB bên trên mặt mũi bằng.
2. Tìm trung điểm của đoạn trực tiếp AB bằng phương pháp phân chia đoạn AB trở thành nhị phần đều bằng nhau. Ký hiệu trung điểm là M.
3. Vẽ một đường thẳng liền mạch ở qua quýt trung điểm M và vuông góc với đoạn trực tiếp AB. Đường này đó là lối trung trực của đoạn trực tiếp AB.
4. Đường trung trực này tách đoạn trực tiếp AB bên trên trung điểm M và được đặt theo hướng trải qua trung điểm M là vuông góc so với đoạn trực tiếp AB.
5. Kiểm tra lại thành phẩm bằng phương pháp đo góc thân ái lối trung trực và đoạn trực tiếp AB. Nếu góc này là 90 chừng, tức là lối trung trực và đã được xác lập đúng mực.
Đây là cơ hội đơn giản và giản dị và hiệu suất cao nhằm xác lập lối trung trực của một quãng trực tiếp.

Đường trung trực của một quãng trực tiếp đem những đặc thù sau:
1. Đường trung trực là đường thẳng liền mạch vuông góc với đoạn trực tiếp ban sơ bên trên trung điểm của đoạn trực tiếp tê liệt.
2. Đường trung trực phân chia đoạn trực tiếp trở thành nhị phần đều bằng nhau về chừng nhiều năm.
3. Một điểm phía trên lối trung trực của một quãng trực tiếp cơ hội đều nhị đầu mút của đoạn trực tiếp tê liệt.
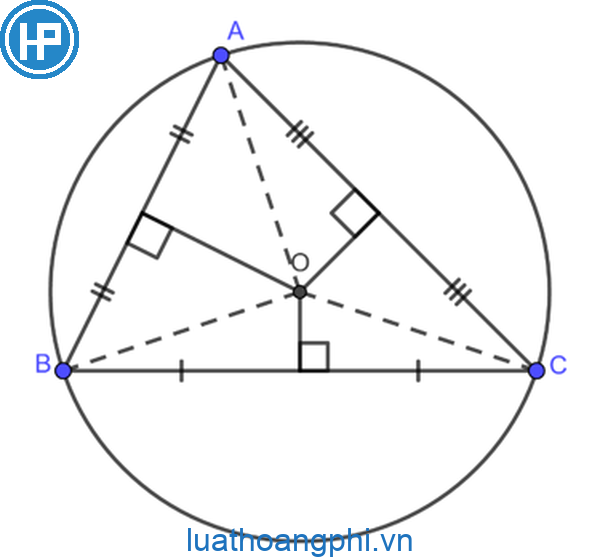
4. Các lối trung trực của những đoạn trực tiếp tách nhau bên trên một điểm độc nhất, được gọi là trung tâm của những đoạn trực tiếp tê liệt.
5. Nếu mang trong mình 1 điểm phía trên lối trung trực của một quãng trực tiếp, thì điểm này đó là trung điểm của đoạn trực tiếp tê liệt.
6. Đường trung trực của một quãng trực tiếp cũng chính là lối trung trực của nhị dặm điểm đối xứng của đoạn trực tiếp tê liệt qua quýt điểm tê liệt.
7. Đường trung trực của một quãng trực tiếp cũng chính là lối đối xứng của đoạn trực tiếp tê liệt qua quýt trung điểm của chính nó.
Đây là những đặc thù cơ bạn dạng của lối trung trực, và nó rất hữu ích trong các việc xử lý những vấn đề tương quan cho tới hình học tập.

Xem thêm: bút bi viết chữ đẹp

Đường trung trực của một quãng trực tiếp đem uỷ thác điểm với đoạn trực tiếp tê liệt, và uỷ thác đặc điểm này nằm ở vị trí trung điểm của đoạn trực tiếp ban sơ. Như vậy rất có thể được chứng tỏ bằng phương pháp dùng khái niệm của lối trung trực.
Để chứng tỏ điều này, tớ cần phải biết rằng lối trung trực của một quãng trực tiếp là một trong đường thẳng liền mạch vuông góc với đoạn trực tiếp ấy bên trên trung điểm của chính nó. Do tê liệt, nút giao điểm của lối trung trực với đoạn trực tiếp ban sơ đó là trung điểm của đoạn trực tiếp tê liệt.
Ví dụ, fake sử tất cả chúng ta đem đoạn trực tiếp AB. Để mò mẫm lối trung trực của AB, trước tiên tớ cần thiết mò mẫm trung điểm M của AB. Sau tê liệt, tớ vẽ một quãng trực tiếp vuông góc với đoạn trực tiếp AB bên trên điểm M. Đoạn trực tiếp mới mẻ này được xem là lối trung trực của đoạn trực tiếp AB. Điểm uỷ thác điểm của lối trung trực này với đoạn trực tiếp AB đó là trung điểm M.
Vậy rằng công cộng, lối trung trực của một quãng trực tiếp đem uỷ thác điểm với đoạn trực tiếp tê liệt, và uỷ thác đặc điểm này nằm ở vị trí trung điểm của đoạn trực tiếp ban sơ.

Đường trung trực của một quãng trực tiếp ko vuông góc với tê liệt. Đường trung trực của một quãng trực tiếp là đường thẳng liền mạch trải qua trung điểm của đoạn trực tiếp và ở vuông góc với đoạn trực tiếp tê liệt. Như vậy rất có thể được chứng tỏ vị toan lý hình học tập rằng lối trung trực tách đoạn trực tiếp trở thành nhị phần đem nằm trong chừng nhiều năm.

Để vẽ lối trung trực của một quãng trực tiếp Lúc chỉ mất nhị điểm bên trên đoạn trực tiếp tê liệt, tớ triển khai công việc sau đây:
Bước 1: Vẽ đoạn trực tiếp AB với nhị điểm A và B vẫn cho tới.
Bước 2: Tìm trung điểm của đoạn trực tiếp AB. Để thực hiện điều này, tớ lấy thành phần khoảng của những tọa chừng của nhị điểm A và B. Ví dụ, nếu như A đem tọa chừng (x1, y1) và B đem tọa chừng (x2, y2), thì trung điểm M đem tọa chừng ((x1 + x2)/2, (y1 + y2)/2).
Bước 3: Vẽ đường thẳng liền mạch trải qua trung điểm M. Đường trực tiếp này được xem là lối trung trực của đoạn trực tiếp AB.
Bước 4: Vẽ mũi thương hiệu ở nhị mút của đoạn trực tiếp AB nhằm chứng thật chiều của đoạn trực tiếp.
Bước 5: Kiểm tra lại loại thị vẫn vẽ nhằm đảm nói rằng lối trung trực vừa phải vẽ tách đoạn trực tiếp AB vuông góc bên trên trung điểm của chính nó.
Với công việc bên trên, bạn đã sở hữu thể vẽ được lối trung trực của một quãng trực tiếp Lúc chỉ biết nhị điểm bên trên đoạn trực tiếp tê liệt.

Xem thêm: bác hồ người cho em tất cả

Đường trung trực của một quãng trực tiếp và đoạn trực tiếp tê liệt đem quan hệ như sau:
1. Đường trung trực của một quãng trực tiếp là đường thẳng liền mạch vuông góc với đoạn trực tiếp tê liệt bên trên trung điểm của chính nó.
2. Một đoạn trực tiếp mang trong mình 1 và có một lối trung trực.
3. Đường trung trực phân chia đoạn trực tiếp ban sơ trở thành nhị phần có tính nhiều năm đều bằng nhau.
4. Mọi điểm bên trên lối trung trực cơ hội đều nhị mút của đoạn trực tiếp.
5. Khi biết nhị đầu mút của đoạn trực tiếp, tớ rất có thể xác lập được lối trung trực.
6. Nếu biết lối trung trực và một điểm bên trên lối trung trực, tớ rất có thể xác lập được đoạn trực tiếp ban sơ.
Đường trung trực của một quãng trực tiếp đem tầm quan trọng cần thiết nhập hình học tập và được dùng rộng thoải mái trong các việc xác lập những thông số kỹ thuật và đối sánh của đoạn trực tiếp cũng như các đối tượng người tiêu dùng hình học tập không giống.

Ứng dụng của lý thuyết lối trung trực nhập thực tiễn là đặc biệt đa dạng và cần thiết trong tương đối nhiều nghành nghề không giống nhau. Dưới đó là một vài ví dụ về kiểu cách dùng lý thuyết lối trung trực nhập thực tế:
1. Trong bản vẽ xây dựng và xây dựng: Lý thuyết lối trung trực được dùng nhằm xác xác định trí những đường đi, công trình xây dựng hoặc hạ tầng. Khi thi công một tòa mái ấm hoặc công trình xây dựng không giống, lối trung trực của những đoạn trực tiếp rất có thể được dùng nhằm xác định những điểm cần thiết, phân loại không khí hoặc đưa đến quy mô phối cảnh.
2. Trong thống kê giám sát và thăm hỏi dò: Lý thuyết lối trung trực cũng rất được dùng trong các việc thống kê giám sát và thăm hỏi dò xét địa hình. Kỹ sư thống kê giám sát rất có thể dùng lối trung trực nhằm xác xác định trí của những điểm nhập không khí phụ vương chiều, và những kỹ sư thăm hỏi dò xét rất có thể dùng nó nhằm xác triết lý dịch rời và khoảng cách.
3. Trong xác định và toan hướng: Lý thuyết lối trung trực cũng rất được dùng trong số phần mềm xác định và triết lý. Ví dụ, nhập khối hệ thống xác định toàn thế giới (GPS), nguyên tắc lối trung trực được dùng nhằm đo lường và tính toán địa điểm của người tiêu dùng dựa vào tín hiệu kể từ những vệ tinh nghịch.
4. Trong hình đồ họa và thiết kế: Lý thuyết lối trung trực cũng rất được dùng nhập hình đồ họa và kiến thiết. Nó được dùng sẽ tạo đi ra những đường thẳng liền mạch hoặc hình học tập chuẩn chỉnh xác, đối xứng hoặc phân loại không khí một cơ hội thích mắt và đúng mực.
5. Trong technology và máy móc: Lý thuyết lối trung trực được dùng trong tương đối nhiều phần mềm technology và công cụ. Ví dụ, nó rất có thể được dùng sẽ tạo đi ra những bạn dạng loại mạch năng lượng điện, kiến thiết những phần tử công cụ hoặc xác xác định trí những cỗ trộn hoặc cảm ứng trong số vũ khí tự động hóa.
Tóm lại, lý thuyết lối trung trực có tương đối nhiều phần mềm cần thiết nhập thực tiễn, kể từ thi công, thống kê giám sát và thăm hỏi dò xét, xác định triết lý, cho tới hình đồ họa và kiến thiết, technology và công cụ. Sử dụng lý thuyết này gom tất cả chúng ta xác xác định trí, thi công kiến thiết đúng mực và tăng nhanh hiệu suất thao tác làm việc trong tương đối nhiều nghành nghề không giống nhau.