tính chất đường cao trong tam giác cân

Tam giác đều, tam giác cân nặng, tam giác vuông là những fake thiết về hình học tập trở thành đặc biệt không xa lạ với tất cả chúng ta vô môn Toán tuy nhiên người nào cũng rất cần phải biết. Bài viết lách tiếp sau đây của Cửa Hàng chúng tôi ham muốn ra mắt cho tới chúng ta những Tích Chất & Cách Tính Đường Cao Tam Giác Đều, Vuông, Cân và những đặc điểm riêng biệt của bọn chúng nhé!

Bạn đang xem: tính chất đường cao trong tam giác cân

1. Một số đặc thù về đàng cao vô tam giác 

Trước tiên bọn chúng hiểu đàng cao vô tam giác đó là đoạn trực tiếp vuông góc xuất phát điểm từ đỉnh của tam giác cho tới cạnh lòng đối lập của tam giác cơ. Mỗi một tam giác sẽ sở hữu được 3 đàng cao và khoảng cách thân ái đỉnh và cạnh lòng là phỏng lâu năm đàng cao. Cùng thăm dò hiểu với Cửa Hàng chúng tôi một trong những đặc thù trong số loại tam giác quan trọng tại đây. 

1.1 Tính hóa học phụ thân đàng cao vô tam giác thường

Cùng với fake thiết đề vấn đề và thành quả và đã được những mái ấm toán học tập bên trên toàn trái đất vẫn minh chứng đã có sẵn. Hiện ni, tất cả chúng ta vẫn quá nhận những tích hóa học của đàng cao vô tam giác thông thường như sau. Ba đàng cao của một tam giác tiếp tục giao phó nhau bên trên một điểm. Và giao phó điểm của phụ thân đàng cao sẽ tiến hành xem là trực tâm của tam giác cơ. 

Tính hóa học phụ thân đàng cao vô tam giác thường

1.2 Tính hóa học đàng cao vô tam giác vuông

Đối với tam giác vuông, đấy là tam giác quan trọng đối với tam giác thông thường bởi vì nó mang trong mình một góc vuông. Chính điều này làm cho đường cao tam giác vuông sẽ sở hữu được một trong những đặc thù khác lạ như tại đây. Những đặc thù này tất cả chúng ta rất cần phải ghi ghi nhớ nhằm sở dĩ rất có thể mang lại lợi ích vô quy trình thực hiện bài xích tập dượt và phần mềm vô cuộc sống thường ngày nhé: 

• Tính hóa học loại 1: Trong tam giác vuông, tích của đàng cao với cạnh huyền ứng chủ yếu vày tích của nhì cạnh góc vuông vô tam giác
• Tính hóa học loại 2: Trong tam giác vuông tao đem bình phương của cạnh góc vuông vày cạnh huyền nhân đàng cao ứng chiếu bên trên cạnh huyền đó
• Tính hóa học loại 3: Trong tam giác vuông, bình phương của đàng cao bên trên cạnh huyền chủ yếu vày tích của nhì hình chiếu bên trên cạnh huyền của nhì cạnh góc vuông 
• Tính hóa học loại 4: Trong tam giác vuông, nghịch ngợm hòn đảo của bình phương từng cạnh góc vuông vày nghịch ngợm hòn đảo của bình phương đàng cao

1.3 Tính hóa học đàng cao vô tam giác cân

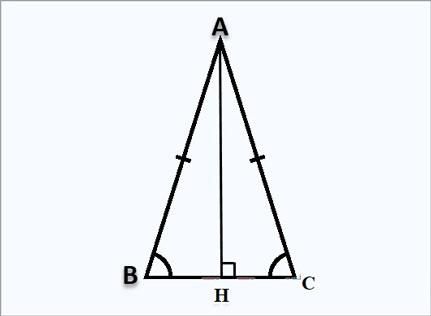
Đường cao vô tam giác cân

Tam giác cân nặng đó là tam giác đem đặc thù nhất là có tính lâu năm nhì cạnh mặt mày đều nhau và 2 góc ở lòng cũng đều nhau. Chính bởi vậy, Đường cao vô tam giác cân sẽ sở hữu được một trong những đặc thù quan trọng tuy nhiên chúng ta học tập cần phải biết như sau:

• Đầu tiên, đàng cao vô tam giác đó là đoạn trực tiếp vuông góc xuất phát điểm từ đỉnh cho tới cạnh lòng. Và đàng cao vô tam giác cân nặng sẽ hỗ trợ phân tách tam giác cân nặng này trở nên 2 tam giác thăng bằng nhau không giống.
• Thứ nhì, đàng cao xuất phát điểm từ đỉnh ứng với cạnh lòng đem chân đàng cao là trung điểm của cạnh lòng. Do cơ nó đôi khi là đàng cao, đàng phân giác và cũng chính là đàng trung trực của tam giác cân nặng.

Bên cạnh cơ, vô tam giác vuông cân nặng là tình huống quan trọng của tam giác cân nặng và tam giác vuông. Chính vậy tuy nhiên, đường cao tam giác vuông cân nặng sẽ có những đặc thù tương tự động như vô tam giác cân nặng và tam giác vuông. Và đàng cao vô tam giác vuông cân nặng tiếp tục phân tách tam giác trở nên nhì tam giác vuông cân nặng.

1.4 Đường cao vô tam giác đều phải sở hữu đặc thù gì?

Tam giác đều là tam giác thông thường đáp ứng nhu cầu đầy đủ những ĐK là đem 3 cạnh đều nhau. Đồng thời 3 góc đem vô tam giác đều vày và vày 60 phỏng nên phỏng lâu năm của 3 đường cao tam giác đều đều nhau. Ngoài ra, đàng cao của tam giác đều phải sở hữu một trong những đặc thù quan trọng nổi trội tuy nhiên chúng ta nên biết như sau: 

Xem thêm: khách sạn sầm sơn gần biển

• Thứ nhất, một tam giác đều phải sở hữu cho tới 3 đàng cao. Và những đàng cao ứng đều xuất phát điểm từ những quyết định và kẻ vuông góc xuống những cạnh lòng sót lại ứng vô tam giác.
• Thứ nhì, 3 đàng cao vô tam giác đều tiếp tục phân tách song những góc ở đỉnh trở nên 2 góc đều nhau và đều vày 30^o
• Thứ phụ thân, đàng cao vô tam giác đều không những đôi khi là đàng trung trực, đàng phân giác tuy nhiên còn là một đàng trung tuyến vô tam giác. Bởi vô tam giác đều sẽ sở hữu được những cạnh đều nhau và những góc đều nhau.
• Thứ tư, đàng cao trải qua trung điểm của cạnh lòng và phân tách cạnh lòng trở nên 2 phần đều nhau.
• Thứ năm, từng đàng cao vô tam giác đều tiếp tục phân tách tam giác trở nên 2 tam giác đều nhau đem diện tích S như nhau tương tự tam giác cân nặng và tam giác vuông.

2. Các công thức tính phỏng lâu năm đàng cao vô tam giác

Hiện ni, những công thức tính phỏng lâu năm đàng cao đều và đã được vạc hiện nay và minh chứng tự những mái ấm toán học tập thời trước. Bởi vậy tuy nhiên trong quy trình giải bài xích tập dượt, chứ không tất cả chúng ta cần minh chứng những công thức lại từ trên đầu nhằm thăm dò ra sức thức thì tất cả chúng ta rất có thể ghi ghi nhớ và vận dụng một trong những công thức tại đây nhằm thăm dò đi ra đáp án thời gian nhanh và đúng đắn rộng lớn nhé!

2.1 Tìm hiểu công thức tính đàng cao vô tam giác ko đặc biệt

Chúng tao rất có thể nhận biết đặc biệt giản dị tam giác thông thường đem 3 cạnh không giống nhau, tạm thời gọi bọn chúng là a, b, c, suy đi ra nửa chu vi p = (a + b + c)/2. Từ cơ tao đem công thức tính độ cao vô tam giác thông thường như sau: h= 2. p p-ap-b(p-c)a 

2.2 Cách tính đàng cao vô tam giác đều thời gian nhanh gọn

Tính đàng cao tam giác đều và hình vẽ đàng cao vô tam giác đều

Tam giác đều là tam giác đem phụ thân cạnh đều nhau và phụ thân góc đều nhau, Chính vậy mà  so với đàng cao vô tam giác đều thì đặc thù cố hữu của đàng cao này đó là 3 đàng cao vô tam giác đều phải sở hữu phỏng lâu năm đều nhau. Và đem đẫy tương đối đầy đủ những đặc thù tương tự nhau.

Do cơ, fake sử cạnh của tam giác đều phải sở hữu phỏng lâu năm là x thì đàng cao vô tam giác đều tiếp tục rất có thể được xem theo gót công thức vẫn minh chứng như sau:  H = x. 32. 

2.3 Một số phương pháp tính đàng cao vô tam giác vuông

Dựa vô những đặc thù vẫn minh chứng của đàng cao vô tam giác vuông thì đường cao vô tam giác vuông tao rút đi ra được một trong những cơ hội tính phỏng lâu năm đàng cao vô tam giác vuông tuy nhiên chúng ta nên biết như sau:

• X. H = Y.Z (theo cơ X,Y,Z thứu tự là những cạnh của tam giác vuông, X là cạnh huyền)
• H² = Y’. Z’ (Y’, Z’ thứu tự là hình chiếu của những cạnh góc vuông bên trên cạnh huyền)
• 1H2 = 1Y2 + 1Z2

2.4 Công thức, phương pháp tính đàng cao vô tam giác cân nặng giản dị nhất

Đối với  tam giác cân nặng là tam giác đem nhì cạnh mặt mày đều nhau và nhì góc mặt mày đều nhau. Chính vì vậy tuy nhiên đàng cao vô tam giác cân nặng đem những đặc thù khác lạ với tam giác thông thường. Do vậy, công thức tính đàng cao của tam giác cân nặng đem phương pháp tính không giống nhau rõ ràng như sau: 

Xem thêm: cách lấy lại zalo trên điện thoại

Giả sử tam giác cân nặng đem 2 cạnh mặt mày có tính lâu năm vày a, cạnh lòng vày b. Từ cơ phụ thuộc đặc thù trung điểm rưa rứa quyết định lí Pi- ta-go tất cả chúng ta đem công thức tính đường cao tam giác cân như sau:

H = 4a2- b24

Như vậy, nội dung bài viết bên trên vẫn giúp cho bạn nhận thêm những kỹ năng và kiến thức hữu ích về những Tính Chất & Cách Tính Đường Cao Tam Giác Đều, Vuông, Cân ở lớp 7. Và tiếp theo sau tất cả chúng ta tiếp tục thích nghi với những đặc thù của tam giác đồng dạng lớp 8. Hãy nối tiếp theo gót dõi Cửa Hàng chúng tôi nhằm hiểu thêm những vấn đề không giống về toán học tập nhé.