Số nguyên

Cấu trúc đại số → lý thuyết nhóm
Lý thuyết nhóm

Thuật ngữ cơ bản

Nhóm con
Nhóm con cái chuẩn chỉnh tắc

Nhóm thương
Tích trực tiếp
Tích nửa trực tiếp

Đồng cấu nhóm

hạt nhân
ảnh
tổng trực tiếp

tích bện
đơn
hữu hạn

vô hạn
liên tục
nhân

cộng tính
cyclic
giao hoán
nhị diện

lũy linh
giải được
tác động

Từ vựng người sử dụng nhập lý thuyết nhóm
Danh sách những chủ thể nhập lý thuyết nhóm

Nhóm hữu hạn

Bạn đang xem: tập hợp z là gì

Phân loại group đơn hữu hạn
cyclic thay phiên dạng Lie sporadic
định lý Cauchy định lý Lagrange Định lý Sylow Định lý Hall p-nhóm Nhóm abel sơ cấp Nhóm Frobenius Nhân tử Schur
Nhóm Mathieu M₁₁ M₁₂ M₂₂ M₂₃ M₂₄ Nhóm Conway Co₁ Co₂ Co₃ Nhóm Janko J₁ J₂ J₃ J₄ Nhóm Fischer F₂₂ F₂₃ F₂₄
nhóm đối xứng S_n Nhóm tứ Klein V Nhóm nhị diện D_n Nhóm Quaternion Q Nhóm Dicyclic Dic_n

Nhóm tách rạc
Lưới

Số vẹn toàn ()
Nhóm tự động do

Nhóm tế bào đun

PSL(2, )
SL(2, )

Nhóm số học
Lưới
Nhóm hyperbolic

Tô pô và group Lie

Solenoid
Đường tròn

Tuyến tính tổng quát mắng GL(n)

Tuyến tính quan trọng SL(n)

Trực gửi gắm O(n)

Euclid E(n)

Trực gửi gắm quan trọng SO(n)

Unita U(n)

Unita quan trọng SU(n)

Symplectic Sp(n)

G₂
F₄
E₆
E₇
E₈

Lorentz
Poincaré
Bảo giác

Vi đồng phôi
Vòng

Nhóm Lie vô hạn chiều

O(∞)
SU(∞)
Sp(∞)

Nhóm đại số

Nhóm đại số tuyến tính

Nhóm khả quy

Đa tạp gửi gắm hoán

Đường cong elliptic

Trong toán học tập, số nguyên được khái niệm một cơ hội thông thườn là một vài hoàn toàn có thể được ghi chép nhưng mà không tồn tại bộ phận phân số. Ví dụ: 21, 4, 0 và −2048 là những số vẹn toàn, trong lúc 9.75, 5 1/2 và ko nên là số vẹn toàn.

Tập hợp ý những số vẹn toàn bao hàm 0, những số bất ngờ dương (1, 2, 3,...), còn được gọi là số đếm,^[1]^[1] và những nghịch ngợm hòn đảo phép tắc nằm trong của bọn chúng (là những số vẹn toàn âm, tức là, −1, −2, −3, ...). Tập hợp ý những số vẹn toàn thông thường được biểu thị bằng văn bản in đậm (Z) hoặc chữ rộng lớn sở hữu viền với vần âm "Z" bắt mối cung cấp kể từ giờ Đức Zahlen (nghĩa là "số").^[2]^[3]^[4]^[5] là một trong tụ hội con cái của tụ hội những số hữu tỷ , cho tới lượt nó là một trong tụ hội con cái của tụ hội những số thực . Giống như tụ hội những số bất ngờ, là tụ hội vô hạn kiểm điểm được.

Các số vẹn toàn tạo ra trở thành group nhỏ nhất và vòng nhỏ nhất chứa chấp những số bất ngờ. Trong lý thuyết số đại số, những số vẹn toàn đôi lúc được xem là số vẹn toàn hữu tỉ nhằm phân biệt bọn chúng với những số vẹn toàn đại số tổng quát mắng rộng lớn. Trên thực tiễn, số vẹn toàn (hữu tỉ) là số vẹn toàn đại số nhưng mà cũng chính là số hữu tỉ.

Ký hiệu[sửa | sửa mã nguồn]

Biểu tượng hoàn toàn có thể được dùng để làm biểu thị những tụ hội không giống nhau, với cơ hội dùng không giống nhau trong số những người sáng tác không giống nhau: ,^[2] hoặc so với những số vẹn toàn dương, hoặc cho những số vẹn toàn ko âm và cho những số vẹn toàn không giống 0. Một số người sáng tác dùng ký hiệu cho những số vẹn toàn không giống 0, trong lúc những người dân không giống dùng nó cho những số vẹn toàn ko âm hoặc mang lại {–1, 1}. Bên cạnh đó, được dùng nhằm biểu thị luyện những số vẹn toàn modulo p^[2] (tức là luyện những lớp đồng dư của những số nguyên) hoặc luyện những số vẹn toàn p -adic.^[1]^[6]^[7]. chính vì thế nếu còn muốn dùng ký hiệu hoặc ký hiệu thì nên khái niệm lại bên trên đề đánh giá, nếu như bên trên đề không tồn tại khái niệm thì coi như đề này đó là sai. Có một vài bài bác câu hỏi minh chứng quy hấp thụ thông thường hoặc dùng nhằm loại cút tình huống không giống ko.Chúng tớ nên địa thế căn cứ nhập sách giáo khoa lớp 6 thực hiện địa thế căn cứ, nhập sách lớp 6 tụ hội số vẹn toàn chỉ mất kí hiệu là Z nên những lúc tất cả chúng ta mang lại đề nhưng mà sở hữu sử

Tính chất[sửa | sửa mã nguồn]

Các số vẹn toàn hoàn toàn có thể được xem là những điểm tách rộc rạc, cơ hội đều nhau bên trên một trục số lâu năm vô hạn. Tại hình bên trên, những số vẹn toàn ko âm được hiển thị vì như thế blue color lam và số vẹn toàn âm red color.

Giống giống như những số bất ngờ, là tụ hội đóng góp với những phép tắc toán nằm trong và nhân, tức là tổng và tích của nhị số vẹn toàn ngẫu nhiên là một vài vẹn toàn. Tuy nhiên, với việc bao hàm cả những số vẹn toàn âm (và cần thiết là 0), , không như những số bất ngờ, cũng chính là tụ hội đóng góp với phép tắc trừ.^[8]

Các số vẹn toàn tạo ra trở thành một vòng đơn vị chức năng, vốn liếng là vòng cơ bạn dạng nhất, theo đòi nghĩa sau: so với ngẫu nhiên vòng đơn vị chức năng này, đều phải sở hữu một phép tắc đồng cấu độc nhất kể từ những số vẹn toàn nhập vòng này. Thuộc tính phổ quát mắng này, ví dụ là một trong đối tượng người sử dụng ban sơ nhập loại vòng, là đặc thù mang lại vòng .

ko đóng góp với phép tắc phân chia, vì như thế thương của nhị số vẹn toàn (ví dụ: 1 phân chia mang lại 2) hoàn toàn có thể ko là số vẹn toàn. Mặc mặc dù những số bất ngờ là đóng góp với phép tắc lũy quá, tuy nhiên những số vẹn toàn thì ko (vì thành phẩm hoàn toàn có thể là một trong phân số Lúc số nón là âm).

Bảng sau liệt kê một vài đặc điểm cơ bạn dạng của phép tắc nằm trong và phép tắc nhân so với ngẫu nhiên số vẹn toàn a, b và c:

Tính hóa học của phép tắc nằm trong và phép tắc nhân bên trên số nguyên
	Phép cộng	Phép nhân
Tính đóng:	a + b là số nguyên	a × b là số nguyên
Tính kết hợp:	a + (b + c) = (a + b) + c	a × (b × c) = (a × b) × c
Tính gửi gắm hoán:	a + b = b + a	a × b = b × a
Tồn bên trên thành phần đơn vị:	a + 0 = a	a × 1 = a
Tồn bên trên thành phần nghịch ngợm đảo:	a + (−a) = 0	Số vẹn toàn độc nhất sở hữu thành phần nghịch ngợm hòn đảo (gọi là đơn vị) là −1 và 1.
Thuộc tính phân phối:	a × (b + c) = (a × b) + (a × c) và (a + b) × c = (a × c) + (b × c)
Không sở hữu ước số của 0:		Nếu a × b = 0, thì a = 0 hoặc b = 0 (hoặc cả hai)

Trong ngữ điệu của đại số trừu tượng, năm tính chất thứ nhất được liệt kê phía trên xác định rằng là một trong group abel với phép tắc nằm trong. Nó cũng là một trong group cyclic, vì như thế từng số vẹn toàn không giống 0 đều hoàn toàn có thể được ghi chép bên dưới dạng tổng hữu hạn 1 + 1 +... + 1 hoặc (−1) + (−1) +... + (−1). Trên thực tiễn, với phép tắc nằm trong là nhóm tuần trả vô hạn duy nhất — theo đòi tức thị ngẫu nhiên group tuần trả vô hạn này đều là đẳng cấu với .

Bốn tính chất thứ nhất được liệt kê phía trên được chấp nhận nhân bảo rằng cùng theo với phép tắc nhân là một trong monoid gửi gắm hoán. Tuy nhiên, ko nên từng số vẹn toàn đều phải sở hữu nghịch ngợm hòn đảo nhân (như tình huống của số 2), Có nghĩa là với phép tắc nhân ko nên là một trong group.

Tất cả những quy tắc kể từ bảng tính chất bên trên (ngoại trừ quy tắc cuối cùng), Lúc được kết phù hợp với nhau, bảo rằng cùng theo với phép tắc nằm trong và phép tắc nhân là một trong vòng gửi gắm hoán sở hữu thành phần đơn vị chức năng. Nó là vẹn toàn khuôn của toàn bộ những đối tượng người sử dụng của cấu tạo đại số như thế. Chỉ những đẳng thức của biểu thức là đúng trong những mang lại toàn bộ những độ quý hiếm của thay đổi, thì cũng chính là đúng trong những ngẫu nhiên vòng gửi gắm hoán sở hữu đơn vị chức năng này. Một số số vẹn toàn không giống 0 ánh xạ cho tới 0 nhập một vài vòng chắc chắn.

Việc thiếu hụt những ước số của 0 trong số số vẹn toàn (thuộc tính sau cuối nhập bảng) Có nghĩa là vòng gửi gắm hoán là một trong miền vẹn toàn.

Việc thiếu hụt những phép tắc nghịch ngợm hòn đảo của phép tắc nhân, tương tự với thực tiễn là ko nên là đóng góp với phép tắc phân chia, Có nghĩa là không phải là một trong ngôi trường. Trường nhỏ nhất chứa chấp những số vẹn toàn bên dưới dạng một vòng con cái là ngôi trường những số hữu tỉ. Quá trình xây đắp những số hữu tỉ kể từ những số vẹn toàn hoàn toàn có thể được học theo sẽ tạo trở thành ngôi trường phân số của ngẫu nhiên miền vẹn toàn này. Và ngược lại, chính thức kể từ ngôi trường số đại số (phần không ngừng mở rộng của số hữu tỉ), vòng số vẹn toàn của chính nó hoàn toàn có thể được trích xuất, bao hàm như thể vòng con cái của chính nó.

Mặc mặc dù phép tắc phân chia thường thì ko được khái niệm bên trên , phép tắc phân chia "với phần dư" được xác lập bên trên bọn chúng. Nó được gọi là phép tắc phân chia Euclid, và sở hữu đặc điểm cần thiết sau: mang lại nhị số vẹn toàn a và b với b ≠ 0, tồn bên trên những số vẹn toàn q và r độc nhất sao mang lại a = q × b + r và 0 ≤ r < |b|, ở đâu |b| biểu thị độ quý hiếm vô cùng của b.^[9] Số vẹn toàn q được gọi là thương và r được gọi là phần dư của phép tắc phân chia a mang lại b. Thuật toán Euclid nhằm tính ước số cộng đồng lớn số 1 sinh hoạt với cùng 1 chuỗi những phép tắc phân chia Euclid.

Một đợt tiếp nhữa, nhập ngữ điệu của đại số trừu tượng, phần bên trên bảo rằng là một trong vòng Euclid. Như vậy ý niệm rằng là một trong vòng ideal chủ yếu và ngẫu nhiên số vẹn toàn dương nào thì cũng hoàn toàn có thể được ghi chép bên dưới dạng tích của những số yếu tắc theo đòi một cơ hội cơ bạn dạng độc nhất.^[10] Đây là ấn định lý cơ bạn dạng của số học tập.

Thuộc tính lý thuyết loại tự[sửa | sửa mã nguồn]

là một trong tụ hội sở hữu trật tự trọn vẹn không tồn tại số lượng giới hạn bên trên hoặc bên dưới. Thứ tự động của được khái niệm là: :... −3 < −2 < −1 < 0 < 1 < 2 < 3 <... Một số vẹn toàn là dương nếu như nó to hơn 0 và âm nếu như nó nhỏ rộng lớn 0. Số ko (0) được khái niệm là ko âm cũng ko dương.

Thứ tự động của những số vẹn toàn tương quí với những phép tắc toán đại số Theo phong cách sau:

Nếu a < b và c < d, thì a + c < b + d
Nếu a < b và 0 < c, thì ac < bc.

Vì vậy, tớ Kết luận rằng cùng theo với trật tự bên trên là một trong vòng sở hữu trật tự.

Các số vẹn toàn là group abel sở hữu trật tự trọn vẹn ko tầm thông thường độc nhất sở hữu những thành phần dương được bố trí theo đòi trật tự hợp lí.^[11] Như vậy tương tự với tuyên thân phụ rằng ngẫu nhiên vòng Review Noether nào thì cũng là một trong ngôi trường — hoặc một vòng định vị vô nằm trong cần thiết.

Xây dựng[sửa | sửa mã nguồn]

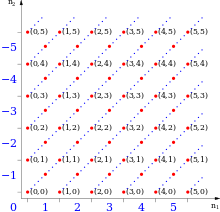
Trong quy trình dạy dỗ học tập ở ngôi trường tè học tập, những số vẹn toàn thông thường được khái niệm một cơ hội trực quan liêu là những số bất ngờ (dương), số 0 và những số đối của những số bất ngờ. Tuy nhiên, loại khái niệm này dẫn theo nhiều tình huống không giống nhau (mỗi phép tắc toán số học tập rất cần phải xác lập bên trên từng tổng hợp những loại số nguyên) và khiến cho việc minh chứng rằng những số vẹn toàn tuân theo đòi những ấn định luật số học tập không giống nhau trở thành tẻ nhạt nhẽo.^[12] Do tê liệt, nhập toán học tập lý thuyết tụ hội văn minh, một cấu tạo trừu tượng hơn^[13] được chấp nhận người tớ xác lập những phép tắc toán số học tập nhưng mà không tồn tại ngẫu nhiên phân biệt tình huống này thông thường được dùng để thay thế thế.^[14] Do tê liệt, những số vẹn toàn hoàn toàn có thể được xây đắp đầu tiên giống như những lớp tương tự của những cặp số bất ngờ sở hữu trật tự (a,b).^[15]

Trực giác là (a,b) là ghi chép tắt của thành phẩm của phép tắc trừ a-b.^[15] Để xác nhận kỳ vọng của tất cả chúng ta rằng 1 − 2 và 4 − 5 biểu thị nằm trong một vài, tất cả chúng ta xác lập mối liên hệ tương tự ~ bên trên những cặp này với quy tắc sau:

Xem thêm: nêu tác dụng của biện pháp tu từ

chỉ khi

Phép nằm trong và phép tắc nhân những số vẹn toàn hoàn toàn có thể được khái niệm theo đòi những phép tắc toán tương tự bên trên những số tự động nhiên;^[15] bằng phương pháp dùng [(a,b)] nhằm biểu thị lớp tương tự sở hữu (a,b) là member, lớp này có:

Số đối (hoặc phép tắc nghịch ngợm hòn đảo của phép tắc cộng) của một vài vẹn toàn đạt được bằng phương pháp hòn đảo ngược trật tự của cặp:

Do tê liệt phép tắc trừ hoàn toàn có thể được khái niệm là phép tắc cùng theo với nghịch ngợm hòn đảo của phép tắc cộng:

Thứ tự động tiêu xài chuẩn chỉnh bên trên những số vẹn toàn được thể hiện với bất đẳng thức:

Lúc và chỉ Lúc

Dễ dàng xác minh rằng những khái niệm này sẽ không tùy theo việc lựa lựa chọn đại diện thay mặt của những lớp tương tự.

Mọi lớp tương tự sở hữu một member độc nhất sở hữu dạng (n,0) hoặc (0,n) (hoặc cả nhị và một lúc). Số bất ngờ n được xác lập với lớp [(n,0)] (nghĩa là, những số bất ngờ được nhúng nhập những số vẹn toàn bằng phương pháp ánh xạ gửi n cho tới [(n,0)]) và lớp [(0,n)] được ký hiệu −n (điều này bao hàm toàn bộ những lớp sót lại và mang lại lớp [(0,0)] gấp đôi bởi −0 = 0.

Do tê liệt, [(a,b)] được ký hiệu là

Nếu những số bất ngờ được xác lập với những số vẹn toàn ứng (sử dụng phép tắc nhúng được rằng ở trên), thì quy ước này sẽ không đưa đến sự mơ hồ nước.

Ký hiệu này bình phục màn trình diễn không xa lạ của những số vẹn toàn là {..., −2, −1, 0, 1, 2,...} {..., −2, −1, 0, 1, 2,...} {..., −2, −1, 0, 1, 2,...} {..., −2, −1, 0, 1, 2,...}.

Một số ví dụ:

Trong khoa học tập PC lý thuyết, những cơ hội tiếp cận không giống nhằm xây đắp những số vẹn toàn được dùng vì như thế những máy dò xét ấn định lý tự động hóa và những khí cụ ghi chép lại thuật ngữ. Số vẹn toàn được màn trình diễn bên dưới dạng những thuật ngữ đại số được xây đắp bằng phương pháp dùng một vài ba phép tắc toán cơ bạn dạng (ví dụ: zero, succ, pred) và, hoàn toàn có thể, dùng những số bất ngờ, được giả thiết là đang được xây đắp (sử dụng cách thức Peano).

Tồn bên trên tối thiểu mươi cơ hội xây đắp những số vẹn toàn sở hữu vết.^[16] Các cấu tạo này không giống nhau theo đòi một vài cách: con số những phép tắc toán cơ bạn dạng được dùng mang lại cấu tạo, con số (thường là kể từ 0 cho tới 2) và những loại đối số được những phép tắc toán này chấp nhận; sự hiện hữu hoặc vắng vẻ mặt mày của những số bất ngờ thực hiện đối số của một vài phép tắc toán này và thực tiễn là những phép tắc toán này còn có nên là hàm tạo ra tự tại hay là không, tức là nằm trong một vài vẹn toàn hoàn toàn có thể được màn trình diễn chỉ vì như thế một hoặc nhiều số hạng đại số.

Kỹ thuật xây đắp những số vẹn toàn được trình diễn phía trên nhập phần này ứng với tình huống ví dụ nhập tê liệt sở hữu một cặp phép tắc toán cơ bạn dạng duy nhất nhận đối số là nhị số bất ngờ và và trả về một vài vẹn toàn (bằng ). Thao tác này sẽ không tự tại vì như thế số vẹn toàn 0 hoàn toàn có thể được ghi chép là cặp (0,0), hoặc cặp (1,1) hoặc cặp (2,2), v.v. Kỹ thuật xây đắp này được dùng vì như thế trợ lý minh chứng Isabelle; tuy vậy, nhiều khí cụ không giống dùng những chuyên môn xây đắp thay cho thế, xứng đáng xem xét là những chuyên môn dựa vào những cấu tạo tự tại, giản dị rộng lớn và hoàn toàn có thể được triển khai hiệu suất cao rộng lớn nhập PC.

Máy tính[sửa | sửa mã nguồn]

Một số vẹn toàn thông thường là một trong loại tài liệu vẹn toàn thủy trong số ngữ điệu PC. Tuy nhiên, loại tài liệu số vẹn toàn chỉ hoàn toàn có thể đại diện thay mặt cho 1 tụ hội con cái của toàn bộ những số vẹn toàn, vì như thế PC thực tiễn sở hữu dung tích hữu hạn. Bên cạnh đó, nhập màn trình diễn phép tắc bù nhị thịnh hành, khái niệm cố hữu của vết phân biệt đằm thắm "âm" và "không âm" thay cho "âm, dương và 0 ". (Tuy nhiên, chắc hẳn rằng PC hoàn toàn có thể xác lập được liệu một độ quý hiếm số vẹn toàn sở hữu thực sự là số dương hay là không.) Các loại tài liệu xấp xỉ số vẹn toàn có tính lâu năm thắt chặt và cố định (hoặc tụ hội con) được ký hiệu là int hoặc Integer nhập một vài ngữ điệu thiết kế (chẳng hạn như Algol68, C, Java, Delphi, v.v..).

Các màn trình diễn số vẹn toàn có tính lâu năm thay cho thay đổi, ví dụ như bignum, hoàn toàn có thể tàng trữ ngẫu nhiên số vẹn toàn này một vừa hai phải với bộ lưu trữ của sản phẩm tính. Các loại tài liệu số vẹn toàn không giống được xây dựng với độ cao thấp thắt chặt và cố định, thông thường là một vài bit là lũy quá của 2 (4, 8, 16, v.v.) hoặc một vài chữ số thập phân (ví dụ: 9 hoặc 10).

Lực lượng[sửa | sửa mã nguồn]

Lực lượng của tụ hội những số vẹn toàn vì như thế ℵ₀ (aleph-null). Điều được đơn giản và dễ dàng minh chứng bằng sự việc xây đắp một tuy vậy ánh, tê liệt là một trong hàm đơn ánh và toàn ánh kể từ cho tới . Nếu như tiếp sau đó đánh giá hàm sau:

{... (−4,8) (−3,6) (−2,4) (−1,2) (0,0) (1,1) (2,3) (3,5)...}

Nếu như thì tớ đánh giá hàm sau:

Xem thêm: lời bài hát xuân đã về

{... (−4,8) (−3,6) (−2,4) (−1,2) (0,1) (1,3) (2,5) (3,7)...}

Nếu miền bị giới hạn nhập vậy thì từng và từng thành phần của sở hữu một và duy nhất thành phần ứng của và theo đòi khái niệm của đồng đẳng lực lượng thì nhị tụ hội này còn có lực lượng cân nhau.

Xem thêm[sửa | sửa mã nguồn]

Số vô tỉ
Số hữu tỉ
Số vẹn toàn tố
Số tự động nhiên
Số đại số
Số siêu việt
Số thực
Số phức
Số siêu phức

Tham khảo[sửa | sửa mã nguồn]

^ ^a ^b ^c Weisstein, Eric W., "Số nguyên" kể từ MathWorld.
^ ^a ^b ^c “Compendium of Mathematical Symbols”. Math Vault (bằng giờ Anh). 1 mon 3 năm 2020. Truy cập ngày 11 mon 8 năm 2020.
^ Weisstein, Eric W. “Integer”. mathworld.wolfram.com (bằng giờ Anh). Truy cập ngày 11 mon 8 năm 2020.
^ Miller, Jeff (29 mon 8 năm 2010). “Earliest Uses of Symbols of Number Theory”. Bản gốc tàng trữ ngày 31 mon một năm 2010. Truy cập ngày trăng tròn mon 9 năm 2010.
^ Peter Jephson Cameron (1998). Introduction to lớn Algebra. Oxford University Press. tr. 4. ISBN 978-0-19-850195-4. Bản gốc tàng trữ ngày 8 mon 12 năm 2016. Truy cập ngày 15 mon hai năm 2016.
^ Keith Pledger and Dave Wilkins, "Edexcel AS and A Level Modular Mathematics: bộ vi xử lý Core Mathematics 1" Pearson 2008
^ LK Turner, FJ BUdden, D Knighton, "Advanced Mathematics", Book 2, Longman 1975.
^ “Integer | mathematics”. Encyclopedia Britannica (bằng giờ Anh). Truy cập ngày 11 mon 8 năm 2020.
^ “The Definitive Higher Math Guide to lớn Long Division and Its Variants — for Integers”. Math Vault (bằng giờ Anh). 24 mon hai năm 2019. Truy cập ngày 11 mon 8 năm 2020.
^ Serge, Lang (1993). Algebra (ấn bạn dạng 3). Addison-Wesley. tr. 86–87. ISBN 978-0-201-55540-0.
^ Warner, Seth (2012). Modern Algebra. Dover Books on Mathematics. Courier Corporation. Theorem trăng tròn.14, p. 185. ISBN 978-0-486-13709-4. Bản gốc tàng trữ ngày 6 mon 9 năm 2015. Truy cập ngày 29 tháng bốn năm 2015.
^ Mendelson, Elliott (2008). Number Systems and the Foundations of Analysis. Dover Books on Mathematics. Courier Dover Publications. tr. 86. ISBN 978-0-486-45792-5. Bản gốc tàng trữ ngày 8 mon 12 năm 2016. Truy cập ngày 15 mon hai năm 2016.
^ Ivorra Castillo: Álgebra
^ Frobisher, Len (1999). Learning to lớn Teach Number: A Handbook for Students and Teachers in the Primary School. The Stanley Thornes Teaching Primary Maths Series. Nelson Thornes. tr. 126. ISBN 978-0-7487-3515-0. Bản gốc tàng trữ ngày 8 mon 12 năm 2016. Truy cập ngày 15 mon hai năm 2016.
^ ^a ^b ^c Campbell, Howard E. (1970). The structure of arithmetic. Appleton-Century-Crofts. tr. 83. ISBN 978-0-390-16895-5.
^ Garavel, Hubert (2017). On the Most Suitable Axiomatization of Signed Integers. Post-proceedings of the 23rd International Workshop on Algebraic Development Techniques (WADT'2016). Lecture Notes in Computer Science. 10644. Springer. tr. 120–134. doi:10.1007/978-3-319-72044-9_9. Lưu trữ bạn dạng gốc ngày 26 mon một năm 2018. Truy cập ngày 25 mon một năm 2018.