Đường tròn trĩnh nước ngoài tiếp tam giác cân nặng - Tất cả những gì bạn phải biết
Chủ đề Đường tròn trĩnh nước ngoài tiếp tam giác cân: Đường tròn trĩnh nước ngoài tiếp tam giác cân nặng là một trong những định nghĩa cần thiết nhập hình học tập. Khi tam giác cân nặng được nội tiếp vào trong 1 đàng tròn trĩnh, điều này đưa đến một đặc điểm đặc biệt quan trọng. Đường tròn trĩnh nước ngoài tiếp tam giác cân nặng tiếp tục trải qua toàn bộ tía đỉnh của tam giác, hỗ trợ cho tớ dễ dàng và đơn giản xác lập tâm của đàng tròn trĩnh nước ngoài tiếp. Đây là một trong những điểm cần thiết đỡ đần ta làm rõ rộng lớn về tam giác cân nặng và những đặc điểm của chính nó.
Bạn đang xem: tâm đường tròn ngoại tiếp tam giác cân
Tam giác cân nặng sở hữu đặc điểm gì về đàng tròn trĩnh nước ngoài tiếp?
Tam giác cân nặng sở hữu đặc điểm đặc biệt quan trọng về đàng tròn trĩnh nước ngoài tiếp. Điều thứ nhất nên biết là tam giác cân nặng sở hữu nhì cạnh đều nhau và nhì góc ở đỉnh đối lập với nhì cạnh này cũng đều nhau.
Để dò xét đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng, tớ dùng đặc điểm của đàng tròn trĩnh nước ngoài tiếp tam giác. Trước tiên, tớ cần thiết dò xét giao phó điểm của đàng trung trực của nhì cạnh đối nhau nhập tam giác cân nặng. Đường trung trực của một cạnh là đường thẳng liền mạch trải qua trung điểm của cạnh cơ và vuông góc với cạnh cơ.
Tìm giao phó điểm của hai tuyến phố trung trực này tiếp tục mang đến tớ tâm của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng. Tâm của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng cũng chính là trung điểm của cạnh đối lập với nhì cạnh đều nhau nhập tam giác cân nặng.
Sau Khi vẫn biết tâm, tớ rất có thể vẽ đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng bằng phương pháp vẽ một đàng tròn trĩnh sở hữu tâm là tâm của tam giác và nửa đường kính vì thế khoảng cách kể từ tâm cho tới 1 trong những tía đỉnh của tam giác.
Tóm lại, đặc điểm của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng là đàng tròn trĩnh này trải qua tía đỉnh của tam giác cân nặng, và tâm của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng là trung điểm của cạnh đối lập với nhì cạnh đồng nhiều năm nhập tam giác cân nặng.
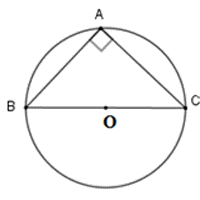
Đường tròn trĩnh nước ngoài tiếp tam giác cân nặng là gì và sở hữu đặc điểm gì quánh biệt?
Đường tròn trĩnh nước ngoài tiếp tam giác cân nặng là đàng tròn trĩnh trải qua 3 đỉnh của tam giác cân nặng. Tính hóa học đặc biệt quan trọng của đàng tròn trĩnh này là tâm của chính nó là trung điểm của đoạn trực tiếp nối nhì đỉnh cân nặng của tam giác và nửa đường kính của đàng tròn trĩnh là phỏng nhiều năm của đoạn nối kể từ tâm cho tới một đỉnh cân nặng. Vấn đề này Có nghĩa là nửa đường kính của đàng tròn trĩnh nước ngoài tiếp tam giác thăng bằng 50% phỏng nhiều năm của cạnh lòng tam giác.
Tâm của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng nằm tại vị trí giao phó điểm của hai tuyến phố trung trực của tam giác cân nặng. Để dò xét tâm của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng, tớ cần thiết tuân theo quá trình sau:
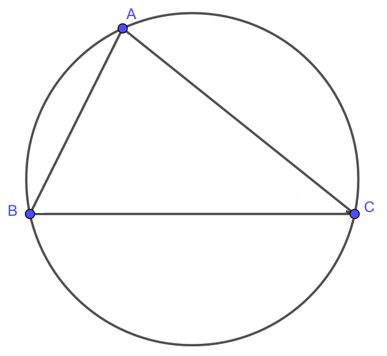
Bước 1: Vẽ tam giác cân nặng ABC với AB = AC.
Bước 2: Xác toan hai tuyến phố trung trực của tam giác, được ký hiệu là đàng trung trực của AB và đàng trung trực của AC.
Bước 3: Kẻ đàng trung trực của AB, trải qua trung điểm của cạnh AB và vuông góc với cạnh AB. Tương tự động, kẻ đàng trung trực của AC, trải qua trung điểm của cạnh AC và vuông góc với cạnh AC.
Bước 4: Giao điểm của hai tuyến phố trung trực là tâm của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng. Ký hiệu tâm là O.
Sau Khi hoàn thành xong quá trình bên trên, tớ vẫn xác lập được tâm của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng.
Toán 9: Hình học- Đường tròn trĩnh nước ngoài tiếp tam giác- Cấp tốc đoạt được đàng tròn
Bạn cũng muốn tò mò vẻ rất đẹp chan chứa bí hiểm của hình học? Xem tức thì đoạn phim này nhằm làm rõ rộng lớn về những hình học tập thú vị và cơ hội bọn chúng tương tác cùng nhau. Quý Khách tiếp tục tò mò rời khỏi rằng hình học tập không chỉ là giản dị và đơn giản thực hiện chúng ta ghi nhớ công thức, nhưng mà nó còn là một trong những tò mò thú vị của trí tuệ thế giới.
Làm thế nào là nhằm dò xét tâm của đàng tròn trĩnh nước ngoài tiếp tam giác cân?
Để dò xét tâm của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng, tớ cần thiết tuân theo quá trình sau:
Bước 1: Vẽ tam giác cân nặng
Đầu tiên, vẽ một tam giác cân nặng với nhì cạnh đều nhau và nhì góc ngược hướng đều nhau. Đặt thương hiệu cho những đỉnh của tam giác là A, B và C.
Bước 2: Tìm trung điểm của cạnh ngẫu nhiên
Chọn một cạnh ngẫu nhiên của tam giác, ví dụ cạnh AB. Tìm trung điểm của cạnh AB và gọi là mang đến trung đặc điểm đó là D.
Bước 3: Tìm đàng trung trực của cạnh AB
Vẽ đường thẳng liền mạch trải qua trung điểm D vuông góc với cạnh AB. Đường trực tiếp này đó là đàng trung trực của cạnh AB. Đặt thương hiệu mang đến giao phó điểm thân thiết đàng trung trực và cạnh AB là O.
Bước 4: Tìm đàng trung trực của cạnh BC
Tương tự động như Cách 3, vẽ đường thẳng liền mạch trải qua trung điểm E của cạnh BC và vuông góc với cạnh BC. Giao điểm thân thiết đàng trung trực của cạnh BC và cạnh BC là Phường.
Bước 5: Tìm giao phó điểm của hai tuyến phố trung trực
Kết hợp ý hai tuyến phố trực tiếp O và Phường, tớ kế tiếp vẽ đường thẳng liền mạch qua quýt O và Phường. Giao điểm thân thiết đường thẳng liền mạch này và cạnh AC là tâm của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng. Đặt thương hiệu mang đến tâm này là T.
Cuối nằm trong, tớ vẫn tìm kiếm ra tâm của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng, được kí hiệu là T.
Đường tròn trĩnh nước ngoài tiếp tam giác cân nặng sở hữu nửa đường kính vì thế bao nhiêu?
Để dò xét nửa đường kính của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng, tớ nên biết đặc điểm đặc thù của tam giác cân nặng.
Một tam giác cân nặng là tam giác sở hữu nhì cạnh đều nhau. Tiếp theo đuổi, dùng đặc điểm đàng tròn trĩnh nước ngoài tiếp tam giác là đàng tròn trĩnh trải qua 3 đỉnh của tam giác.
Vậy, tâm của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng tiếp tục phía trên trục đối xứng của tam giác cân nặng. Trục đối xứng của tam giác cân nặng là đàng trung trực của cạnh lòng.
Vì tam giác cân nặng sở hữu nhì cạnh đều nhau, nên đàng trung trực của cạnh lòng cũng chính là đàng cao của tam giác. Tâm của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng phía trên đàng cao.
Do tam giác cân nặng sở hữu nhì cạnh đều nhau, nên đàng cao của tam giác cũng đó là đàng trung trực của cạnh.
Vậy, nửa đường kính của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng tiếp tục vì thế nửa đoạn dương của đàng cao (đường trung trực của cạnh).
Như vậy, nửa đường kính của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng tiếp tục vì thế nửa đoạn dương của đàng cao (đường trung trực của cạnh).
Xem thêm: lời chúc mừng sinh nhật mẹ

_HOOK_
Tính hóa học của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng trong các việc đo lường những góc và cạnh?
Tính hóa học của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng trong các việc đo lường những góc và cạnh là như sau:
1. Tâm: Tâm của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng là giao phó điểm thân thiết hai tuyến phố trung trực của tam giác, tạo ra trở thành một đàng trung trực cộng đồng.
2. Bán kính: Bán kính của đàng tròn trĩnh nước ngoài tiếp tam giác thăng bằng 50% đàng chéo cánh của tam giác.
3. Góc: Đường tròn trĩnh nước ngoài tiếp tam giác cân nặng tách qua quýt nhì góc lòng của tam giác bên trên những điểm A và B. Vấn đề này Có nghĩa là nhì góc lòng của tam giác cân nặng đều là góc nằm trong cung đồng quỹ của đàng tròn trĩnh nước ngoài tiếp, tức thị bọn chúng sở hữu nằm trong kích cỡ.
4. Cạnh: Cạnh lòng của tam giác cân nặng là 2 lần bán kính của đàng tròn trĩnh nước ngoài tiếp, tức thị cạnh lòng trải qua trung điểm của đàng tròn trĩnh nước ngoài tiếp và vuông góc với cạnh lòng.
Nhờ nhập đặc điểm này, tất cả chúng ta rất có thể dùng đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng nhằm đo lường những góc và cạnh nhập tam giác.
Đường tròn trĩnh nước ngoài tiếp. Đường tròn trĩnh nội tiếp- Bài 8- Toán học tập 9- Cô Vương Thị Hạnh DỄ HIỂU NHẤT
Có khi nào chúng ta tự động chất vấn về đàng tròn trĩnh nước ngoài tiếp và bọn chúng ý nghĩa gì nhập hình học tập không? Hãy coi đoạn phim này nhằm tò mò tình hình thú vị của đàng tròn trĩnh nước ngoài tiếp và dò xét hiểu về việc link của chính nó với những định nghĩa hình học tập không giống. Đây là thời cơ nhằm chúng ta làm rõ rộng lớn về đàng tròn trĩnh và tận thưởng vẻ rất đẹp đương nhiên của chính nó.
Liên hệ thân thiết đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng và đàng tròn trĩnh nội tiếp tam giác cân?
Liên hệ thân thiết đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng và đàng tròn trĩnh nội tiếp tam giác cân nặng như sau:
1. Đường tròn trĩnh nước ngoài tiếp tam giác cân: Đường tròn trĩnh nước ngoài tiếp tam giác cân nặng là đàng tròn trĩnh trải qua tía đỉnh của tam giác cân nặng.
2. Tâm của đàng tròn trĩnh nước ngoài tiếp tam giác cân: Tâm của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng đó là giao phó điểm của tía đàng trung trực của tam giác cân nặng. Điểm này nằm trong là tâm đàng tròn trĩnh nội tiếp tam giác cân nặng.
3. Bán kính của đàng tròn trĩnh nước ngoài tiếp tam giác cân: Bán kính của đàng tròn trĩnh nước ngoài tiếp tam giác thăng bằng nửa đường kính đàng tròn trĩnh nội tiếp tam giác cân nặng và đều vì thế phỏng nhiều năm những đàng kể từ tâm đàng tròn trĩnh nước ngoài tiếp cho tới những đỉnh của tam giác cân nặng.
4. Tư vấn cho tới trái đất thực: Đường tròn trĩnh nước ngoài tiếp tam giác cân nặng và đàng tròn trĩnh nội tiếp tam giác cân nặng sở hữu quan hệ đặc biệt quan trọng cùng nhau, đều trải qua những đỉnh của tam giác cân nặng và share và một tâm. Vấn đề này đã cho chúng ta biết tính đối xứng thân thiết hai tuyến phố tròn trĩnh này và rút rời khỏi được rất nhiều đặc điểm tương quan cho tới tam giác cân nặng.
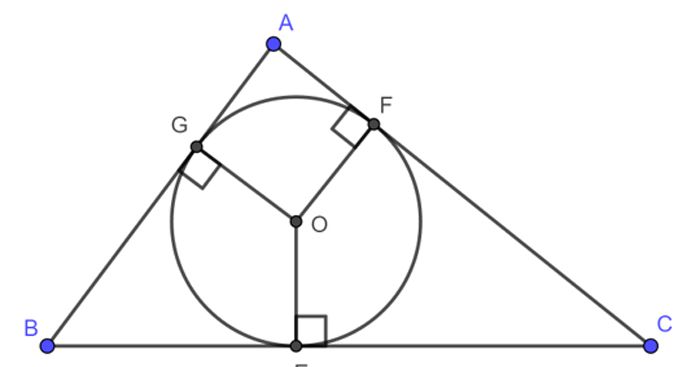
Tại sao đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng được gọi là nước ngoài tiếp?
Đường tròn trĩnh nước ngoài tiếp tam giác cân nặng được gọi là \"ngoại tiếp\" vì thế đàng tròn trĩnh này trải qua toàn bộ tía đỉnh của tam giác cân nặng nhưng mà ko tách hoặc xúc tiếp với ngẫu nhiên cạnh nào là của tam giác. Cụ thể, đàng tròn trĩnh này được xác lập vì thế tâm nằm ở bên trên trung điểm của cạnh lòng tam giác cân nặng và sở hữu nửa đường kính vì thế 50% độ cao của tam giác. Do cơ, đàng tròn trĩnh này \"vây\" hoặc \"bao quanh\" tam giác cân nặng kể từ phía bên ngoài, nên là được gọi là \"ngoại tiếp\".
Xem thêm: lời bài hát đạo làm con
Các phần mềm của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng nhập thực tế?
Các phần mềm của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng nhập thực tiễn rất có thể được nêu rời khỏi như sau:
1. Tính diện tích S tam giác: Khi biết đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng, tớ rất có thể tính được diện tích S của tam giác cơ. Theo công thức: Diện tích tam giác = 50% x cạnh lòng x độ cao, tớ rất có thể xác lập được cạnh lòng và độ cao của tam giác bằng phương pháp dùng những thông số và đo lường và tính toán kể từ nửa đường kính của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng.
2. Tính khoảng cách Một trong những vật thể: Đường tròn trĩnh nước ngoài tiếp tam giác cân nặng rất có thể được dùng nhằm xác lập khoảng cách Một trong những vật thể nhập không khí. bằng phẳng cơ hội biết nửa đường kính của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng và vận dụng những công thức hình học tập, tớ rất có thể đo lường và tính toán được khoảng cách Một trong những vật thể một cơ hội đúng mực.
3. Xác xác định trí tọa độ: Trong hệ tọa phỏng, đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng rất có thể được dùng nhằm xác xác định trí tọa phỏng của những điểm nhập không khí. bằng phẳng cơ hội biết tọa phỏng của những đỉnh tam giác và nửa đường kính của đàng tròn trĩnh nước ngoài tiếp, tớ rất có thể đo lường và tính toán được tọa phỏng của những điểm không giống bên trên đàng tròn trĩnh nước ngoài tiếp.
4. Các phần mềm khác: Đường tròn trĩnh nước ngoài tiếp tam giác cân nặng cũng khá được dùng trong không ít nghành nghề không giống nhau như technology, phong cách thiết kế, kiến thiết hình họa và kiến tạo. Ví dụ, nhập nghành nghề technology, đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng rất có thể được dùng nhằm xử lý những tài liệu không khí và đo lường và tính toán những thông số kỹ thuật chuyên môn. Trong phong cách thiết kế và kiến thiết hình họa, đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng rất có thể được dùng muốn tạo rời khỏi những hình dạng và kiểu đương nhiên, thích mắt. Trên hạ tầng cơ, nhập kiến tạo, đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng cũng rất có thể được dùng nhằm xác xác định trí và đo lường và tính toán những cụ thể trong số dự án công trình kiến tạo.
Tính hóa học cộng đồng của đàng tròn trĩnh nước ngoài tiếp tam giác và tam giác cân? This mix of questions covers the basic understanding, properties, constructions, and applications of the circumcircle of an isosceles triangle.
Tính hóa học cộng đồng của đàng tròn trĩnh nước ngoài tiếp tam giác và tam giác cân nặng là:
1. Đường tròn trĩnh nước ngoài tiếp tam giác là đàng tròn trĩnh được vẽ qua quýt 3 đỉnh của tam giác.
2. Tâm của đàng tròn trĩnh nước ngoài tiếp tam giác là giao phó điểm của 3 đàng trung trực của tam giác.
3. Đường tròn trĩnh nước ngoài tiếp tam giác cân nặng sẽ có được tâm phía trên đàng trung trực của đoạn chéo cánh của tam giác.
4. Đường tròn trĩnh nước ngoài tiếp tam giác cân nặng tiếp tục tách đoạn chân trực góc của tam giác bên trên nhì điểm sở hữu nằm trong khoảng cách cho tới đỉnh góc vuông.
5. Đường kính của đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng tiếp tục đó là đoạn chéo cánh của tam giác.
Đây là những đặc điểm cộng đồng của đàng tròn trĩnh nước ngoài tiếp tam giác và tam giác cân nặng. Những đặc điểm này rất có thể được dùng nhằm giải quyết và xử lý những việc tương quan cho tới tam giác cân nặng và đàng tròn trĩnh nước ngoài tiếp tam giác cân nặng, như đo lường và tính toán 2 lần bán kính, dò xét tâm đàng tròn trĩnh nước ngoài tiếp, hoặc tế bào phỏng địa điểm của những đỉnh tam giác.
_HOOK_









Bình luận