q là tập hợp số gì

Số hữu tỉ là gì? 

Trong toán học tập, số hữu tỉ là những số x hoàn toàn có thể màn biểu diễn bên dưới dạng phân số a/b, vô bại liệt a và b là những số vẹn toàn với b # 0. Tập thích hợp những số hữu tỉ, hoặc còn gọi là ngôi trường số hữu tỉ, với ký hiệu là Q.

Bạn đang xem: q là tập hợp số gì

Số hữu tỉ là số hoàn toàn có thể ghi chép bên dưới dạng a/b với a, b ∈ Z,b ≠ 0 và được kí hiệu là Q.

Ví dụ: Các số 3; -1/2; 2/3;... là những số hữu tỉ

Tập thích hợp số hữu tỉ Q gồm:

• Số thập phân hữu hạn: 0.5 (½), 0.2 (⅕),...

• Số thập phân vô hạn tuần hoàn: 0.16666… (⅙), 0.3333… (⅓),...

• Tập thích hợp số vẹn toàn (Z): -2, -1, 0, 1, 2,...

• Tập thích hợp số đương nhiên (N): 1, 2, 3, 4, 5, 6,…

Tính hóa học của số hữu tỉ là gì vô toán học?

• Tập thích hợp số hữu tỉ q là tập trung kiểm đếm được.

• Phép nhân số hữu tỉ với dạng:

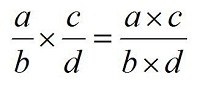
• Phép phân chia số hữu tỉ với dạng:

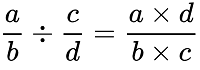
• Nếu số hữu tỉ là số hữu tỉ dương thì số đối của chính nó là số hữu tỉ âm và ngược lại. Tức tống số hữu tỉ và số đối của chính nó vày 0.

Xem thêm: Nguyên hàm từng phần là gì? Công thức tính vẹn toàn hàm từng phần cơ phiên bản và nâng lên tương đối đầy đủ nhất

Phân loại: Tập Q bao gồm những số nào?

Tập thích hợp q là số hữu tỉ, vậy số hữu tỉ là những số nào? Trong toán học tập sẽ sở hữu 2 loại số hữu tỉ, bao hàm số hữu tỉ âm và số hữu tỉ dương. Cụ thể:

• Số hữu tỉ âm: Bao bao gồm những số hữu tỉ nhỏ rộng lớn 0
• Số hữu tỉ dương: Bao bao gồm những tuột hữu tỉ to hơn 0
• Lưu ý: số 0 ko nên là số hữu tỉ âm và cũng ko nên là số hữu tỉ dương.

Các phép tắc toán cơ phiên bản với số hữu tỉ 

Qua phần kỹ năng và kiến thức bên trên chúng ta vẫn bắt được q là tập hợp số gì vô toán. Trong kỹ năng và kiến thức số hữu tỉ toán học tập lớp 7, những em sẽ tiến hành thích nghi với những phép tắc toán cơ phiên bản với q là số hữu tỉ như sau:

Phép tính nằm trong trừ

Sau đó là quá trình tuy nhiên chúng ta cũng có thể vận dụng nhằm tính những phép tắc toán nằm trong trừ với những số hữu tỉ.

Bước 1: Viết những số hữu tỉ bên dưới dạng phân số

Bước 2: sít dụng quy tắc nằm trong, trừ và những đặc thù nhằm tính

Quy tắc nằm trong, trừ: Đưa những số hữu tỉ về nằm trong khuôn (quy đồng, rút gọn gàng,…) rồi nằm trong, trừ tử số, không thay đổi khuôn số.

Tính chất:

• Tính hóa học gửi gắm hoán: x + hắn = hắn + x

• Tính hóa học kết hợp: (x + y) + z = x + (y + z)

• Tính hóa học cùng theo với 0: x + 0 = 0 + x = x

Bước 3: Rút gọn gàng thành phẩm (nếu với thể)

Phép tính nhân chia

• Nhân nhị số hữu tỉ:

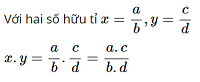
• Chia nhị số hữu tỉ:

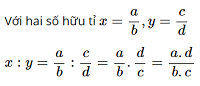
Các phép tắc tính và công thức toán không giống với số hữu tỉ

Bên cạnh những phép tắc tính cơ phiên bản kể bên trên, thì chúng ta còn rất cần phải Note một trong những phép tắc tính và công thức tương quan cho tới số hữu tỉ thông thường bắt gặp sau.

Giá trị vô cùng của một số ít hữu tỉ

Giá trị vô cùng của một trong những hữu tỉ x được kí hiệu là |x|, là khoảng cách kể từ điểm x cho tới điểm O bên trên trục số.

• Nếu x > 0 thì |x| = x.

• Nếu x = 0 thì |x| = 0.

• Nếu x < 0 thì |x| = -x.

Dựa vô khái niệm bên trên, công thức xác lập độ quý hiếm vô cùng của một số ít hữu tỉ như sau:

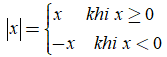
Công thức tính lũy quá của một số ít hữu tỉ:

Các công thức tính lũy quá của một số ít hữu tỉ tuy nhiên bạn phải ghi nhớ:

Cách đối chiếu nhị số hữu tỉ

Để đối chiếu nhị số hữu tỉ x, hắn tao hoàn toàn có thể thực hiện như sau:

• Viết x, hắn bên dưới dạng phân số nằm trong khuôn dương.

x = a /m; hắn = b/m ( m > 0) 

• So sánh những tử là số vẹn toàn a và b

• Nếu a > b thì x > y

  Xem thêm: cân bằng cảm xúc cả lúc bão giông

• Nếu a = b thì x = y

• Nếu a < b thì x < y

Số vô tỉ là gì?

Trong toán học tập, những số vô tỉ là tất cả những số thực ko nên là số hữu tỉ, tuy nhiên là những số được xây đắp kể từ những tỷ số (hoặc phân số) của những số vẹn toàn.

Số vô tỉ kí hiệu là gì? Số vô tỉ là các số ghi chép được bên dưới dạng số thập phân vô hạn ko tuần trả. Và kí hiệu của số vô tỉ là I.

Các bạn phải ghi nhớ các số thực ko nên là số hữu tỉ có tức thị chúng ta ko thể màn biểu diễn được bên dưới dạng tỉ số như a/ b (trong bại liệt a, b là những số nguyên).

Tính hóa học của số vô tỉ: Tập thích hợp số vô tỉ là tập trung ko kiểm đếm được.

Ví dụ:

• Số vô tỉ: 0,1010010001000010000010000001… (đây là số thập phân vô hạn ko tuần hoàn)

• Số căn bậc 2: √2 (căn 2)

• Số pi (π): 3,14159 26535 89793 23846 26433 83279 50 288…..

Sự không giống nhau thân thiết số hữu tỉ và số vô tỉ

• Số hữu tỉ bao hàm số thập phân vô hạn tuần trả, còn số vô tỉ là những số thập phân vô hạn ko tuần trả.

• Số hữu tỉ đơn giản phân số, còn số vô tỉ với thật nhiều loại số không giống nhau

• Số hữu tỉ là số kiểm đếm được, còn số vô tỉ là số ko kiểm đếm được

Các dạng bài bác luyện về luyện Q - Số hữu tỉ và cách thức giải

Tới trên đây, những em vẫn bắt được định nghĩa số hữu tỉ là gì? Tập thích hợp q là ký hiệu gì vô toán học tập. Dưới đó là một trong những dạng bài bác luyện về số hữu tỉ thông thường bắt gặp nằm trong cách thức giải nhằm những em xem thêm và áp dụng:

Dạng 1: Thực hiện tại phép tắc tính với q là số hữu tỉ

Phương pháp giải: Đầu tiên cần thiết ghi chép 2 số hữu tỉ vẫn mang lại bên dưới dạng phân số, rồi tổ chức vận dụng quy tắc đo lường nhằm tính và thể hiện đáp số đúng mực, rưa rứa rút gọn gàng thành phẩm nếu như hoàn toàn có thể.

Lưu ý: Chỉ được vận dụng tính chất:

• a.b + a.c = a.(b+c)
• a.c + b.c = (a+b).c)

Chứ ko được áp dụng: a:b + a:c = a:(b+c)

Ví dụ:

Dạng 2: Biểu thao diễn tập trung q số hữu tỉ bên trên trục số

Phương pháp giải:

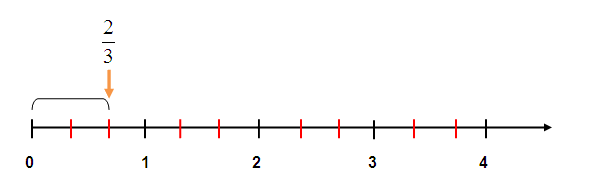
• Trường thích hợp a/b là số hữu tỉ dương: tao tổ chức phân chia khoảng tầm có tính lâu năm 1 đơn vị chức năng thực hiện b phần cân nhau. Sau bại liệt tổ chức lấy về chiều dương trục Ox với a phần. Lúc này tao sẽ tiến hành địa điểm của số a/b.
• Trường thích hợp a/b là số hữu tỉ âm: ta tổ chức phân chia khoảng tầm có tính lâu năm 1 đơn vị chức năng thực hiện b phần cân nhau. Sau bại liệt tổ chức lấy về chiều âm trục Ox với a phần. Lúc này tao sẽ tiến hành địa điểm của số a/b.

Ví dụ: Biểu thao diễn số 5/4

Giải:

Ta thấy 5/4 là số hữu tỉ dương. Lúc này tao phân chia những khoảng tầm ứng với chừng lâu năm 1 đơn vị chức năng thực hiện trở thành 4 phần cân nhau. Lấy 5 phần tao tiếp tục màn biểu diễn được phân số 5/4.

Dạng 3: So sánh những số hữu tỉ q

Phương pháp giải: Ta tiếp tục trả những số hữu tỉ vẫn mang lại bên dưới dạng phân số với nằm trong khuôn số dương rồi đối chiếu tử số. Hình như, những em cũng hoàn toàn có thể đối chiếu với số 0, đối chiếu với số 1, -1 hoặc phụ thuộc phần bù của một, rưa rứa đối chiếu với phân số trung gian ngoan nhằm tìm hiểu đáp án đúng mực.

Ví dụ: So sánh những số hữu tỉ sau:

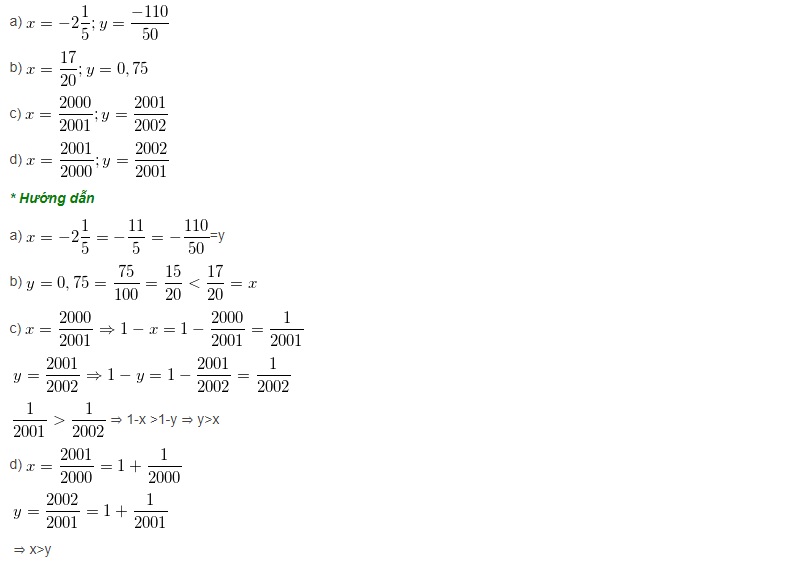
Dạng 4: Tìm ĐK nhằm một trong những hữu tỉ q là âm, dương hoặc là 0

Phương pháp giải: Các em phụ thuộc đặc thù của số hữu tỉ nhằm xác lập được này là số âm, dương Hay những 0.

Ví dụ:

Dạng 5: tìm hiểu những số hữu tỉ trực thuộc một khoảng

Phương pháp giải: Đưa những số hữu tỉ bại liệt về nằm trong khuôn hoặc tử số.

Dạng 6: Tìm x nhằm biểu thức nguyên

Phương pháp giải: Trường thích hợp tử số ko chứa chấp x tao sử dụng vệt phân chia không còn, nếu như tử số chứa chấp x tao sử dụng vệt phân chia không còn hoặc vận dụng cơ hội tách tử số theo gót khuôn số. Đối với những việc tìm hiểu mặt khác cả x và hắn, tao tiếp tục group x hoặc hắn rồi rút bọn chúng trả về dạng phân thức.

Dạng 7: Các việc tìm hiểu x với số hữu tỉ q

Phương pháp giải: Đầu tiên tao nên quy đồng khử khuôn số, rồi gửi những số hạng chứa chấp x về một vế, những số hạng còn sót lại về một vế (chuyển vế thay đổi dấu) rồi tổ chức tìm hiểu x.

Ví dụ:

Dạng 8: Bài toán tìm hiểu x trong những bất phương trình

Phương pháp giải:

Ví dụ: Tìm x, biết:

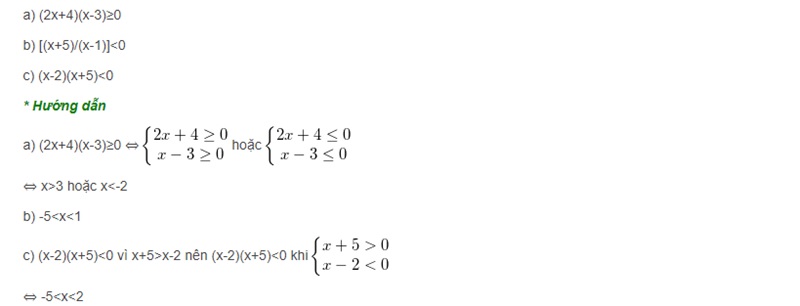
Dạng 9: Các việc tính tổng tập trung q là những số hữu tỉ theo gót quy tắc

* Quy tắc 1: Tính tổng sản phẩm số với những số hạng xa nhau một trong những ko đổi

Phương pháp giải:

* Quy tắc 2: Tính tổng sản phẩm số với những số hạng với số đứng sau hấp tấp n số đứng trước.

Phương pháp giải: Tiến hành phân tách kể từ số trở thành hiệu của 2 số (số cuối – số đầu) phía khuôn số.

Xem thêm: cách tắt quảng cáo trên điện thoại samsung

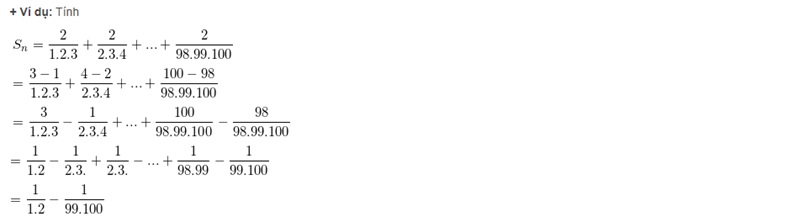
Một số bài bác luyện khuôn về tập trung Q - số hữu tỉ tự động luyện

Hy vọng, trải qua những share bên trên của Monkey tiếp tục giúp đỡ bạn phần nào là nắm rõ không còn định nghĩa và những công thức đo lường về số hữu tỉ và số vô tỉ. Đồng thời, thông qua đó tương hỗ chúng ta xây đắp và thu nhận kỹ năng và kiến thức nâng lên một cơ hội chất lượng tốt rộng lớn bên trên lớp. Xin được sát cánh nằm trong chúng ta.