Đường trung tuyến vô tam giác cân nặng - Bế Tắc quyết giải quyết và xử lý những yếu tố liên quan
Chủ đề Đường trung tuyến vô tam giác cân: Đường trung tuyến vô tam giác cân nặng là một trong đường thẳng liền mạch quan trọng đặc biệt đem tầm quan trọng cần thiết vô tam giác. Nó nối kể từ đỉnh của tam giác cho tới điểm trung điểm của cạnh đối lập, tạo ra trở nên một đường thẳng liền mạch vô tam giác. Đường trung tuyến không chỉ có phân chia tam giác trở nên nhị phân vùng đều nhau, mà còn phải đem theo không ít đặc thù quan trọng đặc biệt khác ví như vuông góc với cạnh lòng, làm cho tam giác cân nặng trở thành thích mắt và mê hoặc.
Bạn đang xem: đường trung tuyến trong tam giác cân
- Đường trung tuyến vô tam giác cân nặng là đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh lòng ứng.
- Tính hóa học của đường trung tuyến trong tam giác cân là:
1. Đường trung tuyến ứng kể từ góc đỉnh tiếp tục vuông góc với cạnh lòng ứng (nó là lối trung trực của cạnh đáy).
2. Hai đường trung tuyến trong tam giác cân tiếp tục hạn chế nhau bên trên một điểm bên trên lối trung trực của cạnh lòng.
3. Hai đường trung tuyến trong tam giác cân đều nhau về phỏng nhiều năm và hạn chế nhau bên trên trung điểm của cạnh lòng.
4. Đường trung tuyến vô tam giác cân nặng là một trong lối tại chính giữa tam giác, phân chia tam giác trở nên nhị tam giác thăng bằng nhau về diện tích S.
5. Đường trung tuyến vô tam giác cân nặng qua loa một điểm bên trên lối trung trực của cạnh lòng và phân chia nó trở nên hai tuyến đường trung trực đối xứng cùng nhau.
6. Đường trung tuyến vô tam giác cân nặng có tính nhiều năm vì chưng 50% phỏng nhiều năm cạnh lòng của tam giác.

Đường trung tuyến vô tam giác cân nặng là gì?
Đường trung tuyến vô tam giác cân nặng là đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh lòng ứng. Đối với cùng một tam giác cân nặng, đem phụ thân lối trung tuyến, từng lối trung tuyến phân chia tam giác trở nên nhị tam giác con cái đem diện tích S đều nhau. Bên cạnh đó, đường trung tuyến trong tam giác cân cũng chính là lối trung trực của cạnh lòng, tức là lối trung tuyến vuông góc với cạnh lòng. Khi vẽ những đường trung tuyến trong tam giác cân, tớ rất có thể nhận biết rằng phụ thân lối trung tuyến hạn chế nhau bên trên một điểm độc nhất, tê liệt đó là trọng tâm của tam giác.
Tam giác cân nặng đem từng nào lối trung tuyến?
Tam giác cân nặng đem 3 lối trung tuyến. Đường trung tuyến vô tam giác cân nặng là đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh đối lập. Cụ thể, từng lối trung tuyến ứng với cùng một cạnh của tam giác cân nặng và phân chia cạnh ấy trở nên nhị đoạn có tính nhiều năm đều nhau. điều đặc biệt, lối trung tuyến ứng kể từ góc đỉnh của tam giác cân nặng tiếp tục vuông góc với cạnh lòng ứng và là lối trung trực của cạnh lòng.
Cách tính phỏng nhiều năm đường trung tuyến trong tam giác cân?
Để tính phỏng nhiều năm đường trung tuyến trong tam giác cân, tớ cần thiết thực hiện như sau:
Bước 1: Xác ấn định đỉnh và lòng của tam giác cân nặng.
Bước 2: Vẽ đường thẳng liền mạch nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh lòng (đường trung tuyến).
Bước 3: Sử dụng công thức khoảng cách thân thuộc nhị điểm vô hệ tọa phỏng nhằm tính phỏng nhiều năm lối trung tuyến.
Giả sử tớ đem tam giác cân nặng ABC với đỉnh A và lòng BC. Gọi M là trung điểm của BC.
Bước 1: Xác ấn định đỉnh và lòng của tam giác cân nặng.
Trong tình huống này, đỉnh là A và lòng là BC.
Bước 2: Vẽ lối trung tuyến kể từ đỉnh A cho tới trung điểm M của cạnh BC.
Vẽ đường thẳng liền mạch AM.
Bước 3: Sử dụng công thức khoảng cách thân thuộc nhị điểm vô hệ tọa phỏng nhằm tính phỏng nhiều năm lối trung tuyến.
Để tính phỏng nhiều năm AM, tớ dùng công thức:
AM = √((x2 - x1)^2 + (y2 - y1)^2)
Trong tê liệt, (x1, y1) là tọa phỏng của điểm A và (x2, y2) là tọa phỏng của điểm M.
Lưu ý rằng, tớ cần phải biết tọa phỏng của những điểm A và M vô tình huống ví dụ nhằm đo lường và tính toán thành phẩm sau cuối.
Nếu đem tọa phỏng của những điểm A và M, tớ thay cho thế vô công thức bên trên và đo lường và tính toán độ quý hiếm của lối trung tuyến AM.
Phân biệt lối trung tuyến, lối trung trực, lối cao, lối phân giác vô tam giác
Đường trung tuyến: Hãy mày mò đoạn phim lạ mắt về đặc thù quan trọng đặc biệt của lối trung tuyến vô tam giác. Nhận tăng kỹ năng và làm rõ rộng lớn về phần mềm thực tiễn của lối trung tuyến vô toán học tập.
Toán 7 - Tính hóa học 3 lối trung tuyến vô tam giác
Tính hóa học 3: quý khách hàng đang được lần hiểu về đặc thù 3 vô toán học? Xem đoạn phim sâu sát này nhằm lần hiểu về những đặc thù thú vị và phần mềm của bọn chúng trong mỗi câu hỏi mê hoặc. Hãy sẵn sàng cho tới bạn dạng thân thuộc một cơ hội chất lượng tốt nhất!
Đường trung tuyến vô tam giác cân nặng đem Điểm lưu ý gì quánh biệt?
Đường trung tuyến vô tam giác cân nặng đem những Điểm lưu ý quan trọng đặc biệt sau:
1. Đường trung tuyến vô tam giác cân nặng là một trong đoạn trực tiếp được vẽ kể từ đỉnh của tam giác cho tới trung điểm của cạnh lòng ứng.
2. Mỗi tam giác cân nặng đem phụ thân lối trung tuyến, từng lối trung tuyến phân chia tam giác trở nên nhị tam giác nhỏ nằm trong diện tích S.
3. Đường trung tuyến vô tam giác cân nặng đem một trong những đặc thù quánh biệt:
- Đường trung tuyến ứng kể từ góc đỉnh của tam giác cân nặng tiếp tục vuông góc với cạnh lòng ứng. Nghĩa là bên trên lối trung tuyến, góc tạo ra vì chưng lối trung tuyến và cạnh lòng là 90 phỏng.
- Đường trung tuyến cũng chính là lối trung trực của cạnh lòng, tức là lối trung tuyến tiếp tục trải qua trung điểm của cạnh lòng và hạn chế cạnh lòng trở nên nhị phần đều nhau.
Đây là những Điểm lưu ý quan trọng đặc biệt của đường trung tuyến trong tam giác cân.
_HOOK_
Tại sao đường trung tuyến trong tam giác cân luôn luôn trải qua tâm lối tròn trĩnh nội tiếp?
Để hiểu tại vì sao đường trung tuyến trong tam giác cân luôn luôn trải qua tâm lối tròn trĩnh nội tiếp, tất cả chúng ta cần thiết lần hiểu về đặc thù quan trọng đặc biệt của tam giác cân nặng và lối trung tuyến.
Đầu tiên, một tam giác cân nặng là tam giác đem nhị cạnh đều nhau và nhị góc ở đỉnh của tam giác thăng bằng nhau. Như vậy Tức là đỉnh của tam giác cân nặng đó là trung tâm của lối tròn trĩnh nội tiếp tam giác.
Tiếp theo gót, tớ xét tam giác cân nặng ABC với AB = AC. Đường trung tuyến vô tam giác này là một trong đoạn trực tiếp nối kể từ đỉnh A cho tới trung điểm M của cạnh BC.
Gọi O là trung điểm của cạnh AB. Ta cần thiết minh chứng rằng điểm O phía trên lối trung tuyến AM.
Để minh chứng điều này, tớ dùng đặc thù của trung điểm, này đó là đường thẳng liền mạch nối một đỉnh của tam giác cho tới trung điểm của cạnh ứng là lối trung trực của cạnh tê liệt. Tại trên đây, tớ đem trung điểm O của cạnh AB là trung điểm của cạnh BC, bởi vậy, AM là lối trung trực của cạnh BC.
Từ đặc thù bên trên, tớ rất có thể Kết luận rằng lối trung tuyến AM vô tam giác cân nặng ABC đó là lối trung trực của cạnh BC.
Điểm O cũng phía trên lối trung trực của cạnh BC, và bởi này cũng phía trên lối trung tuyến AM.
Tóm lại, tớ tiếp tục minh chứng rằng vô tam giác cân nặng, lối trung tuyến luôn luôn trải qua tâm lối tròn trĩnh nội tiếp tam giác.
Tam giác cân nặng đem từng nào góc trung tuyến?
Tam giác cân nặng đem 3 góc trung tuyến. Giả sử tớ đem tam giác ABC với AB = AC. Đường trung tuyến kể từ đỉnh A là đoạn trực tiếp nối điểm trung điểm của cạnh BC cho tới đỉnh A. Do tam giác cân nặng đem nhị cạnh đều nhau, điểm trung điểm của cạnh BC cũng là vấn đề trung điểm của cạnh AB và cạnh AC. Do tê liệt, Lúc nối điểm trung đặc điểm đó cho tới đỉnh A, tớ nhận được đường thẳng liền mạch hạn chế cạnh BC bên trên điểm trung điểm.
Vì đem nhị cạnh đều nhau, tớ đem hai tuyến đường trung tuyến. Tương tự động, nếu như tớ nối điểm trung điểm của những cạnh AB, BC và AC cho tới những đỉnh ứng, tớ cũng tiếp tục nhận được hai tuyến đường trung tuyến. Tổng nằm trong, tam giác cân nặng đem 3 góc trung tuyến.
Đường trung tuyến vô tam giác cân nặng ứng với lòng tam giác được xem là lối trung trực của cạnh lòng, tức là đường thẳng liền mạch phân chia song cạnh lòng và vuông góc với cạnh lòng.
Đường trung tuyến của tam giác cân nặng đem vuông góc với cạnh lòng không?
Đường trung tuyến của tam giác cân nặng đem vuông góc với cạnh lòng.
Để minh chứng điều này, tớ tiếp tục dùng đặc thù lối trung tuyến của tam giác cân nặng.
Đường trung tuyến của tam giác cân nặng là đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh lòng ứng.
Như vậy, tớ mang 1 tam giác cân nặng ABC với đỉnh A, lòng BC và trung điểm M của cạnh BC. Đường trung tuyến của tam giác cân nặng này là đường thẳng liền mạch AM.
Theo đặc thù lối trung tuyến của tam giác cân nặng, lối trung tuyến AM tiếp tục vuông góc với cạnh lòng BC.
Vậy, tớ có: Đường trung tuyến của tam giác cân nặng đem vuông góc với cạnh lòng.
Các đặc thù quan trọng đặc biệt của đường trung tuyến trong tam giác cân?
Các đặc thù quan trọng đặc biệt của đường trung tuyến trong tam giác cân như sau:
1. Đường trung tuyến vô tam giác cân nặng là đoạn trực tiếp nối kể từ đỉnh (góc đỉnh) của tam giác cho tới trung điểm của cạnh lòng (cạnh bên).
2. Đường trung tuyến không chỉ có là đoạn trực tiếp, tuy nhiên còn là một lối trung trực của cạnh lòng. Như vậy Tức là lối trung tuyến tiếp tục vuông góc với cạnh lòng của tam giác cân nặng.
3. Đường trung tuyến vô tam giác cân nặng tiếp tục hạn chế nhau bên trên một điểm độc nhất, gọi là trọng tâm của tam giác. Trọng tâm là trung điểm của toàn bộ những đoạn trực tiếp nối kể từ những đỉnh của tam giác cho tới trung điểm của những cạnh đối lập.
4. Đường trung tuyến kể từ góc đỉnh của tam giác cân nặng tiếp tục phân chia tam giác trở nên nhị tam giác cân nặng nhau. Như vậy Tức là cả tam giác gốc và nhị tam giác con cái đem lối trung tuyến là những đoạn trực tiếp đem nằm trong phỏng nhiều năm.
5. Đường trung tuyến vô tam giác cân nặng trải qua trọng tâm, điều này còn có ý nghĩa sâu sắc cần thiết trong những việc lần trọng tâm và phần mềm của chính nó vô giải toán tam giác.
Những đặc thù quan trọng đặc biệt này chung tất cả chúng ta làm rõ rộng lớn về đường trung tuyến trong tam giác cân và cơ hội nó tác dụng cho tới những nhân tố không giống vô tam giác.
Xem thêm: câu bị đông là gì tiếng việt

Tính hóa học phụ thân lối trung tuyến của tam giác - Bài 4 - Toán học tập 7 - Cô Nguyễn Thu Hà
Ba lối trung tuyến: Hãy mày mò đoạn phim thú vị này về phụ thân lối trung tuyến vô tam giác. Tìm hiểu những đặc thù quan trọng đặc biệt của bọn chúng và cơ hội bọn chúng tạo ra những hình học tập mê hoặc vô toán học tập. Đừng bỏ qua thời cơ này!
Toán nâng lên lớp 7 - Tính hóa học phụ thân lối trung tuyến của tam giác - thầy Nguyễn Thành Long
Toán nâng cao: Nếu các bạn đang được quan hoài cho tới toán nâng lên, đoạn phim này chắc hẳn rằng là một trong điểm đến chọn lựa hoàn hảo. Với những yếu tố phức tạp và những câu hỏi thử thách, đoạn phim tiếp tục giúp cho bạn nắm rõ kỹ năng và nâng cấp kỹ năng giải quyết và xử lý những câu hỏi toán nâng lên.
Đường trung tuyến vô tam giác cân nặng rất có thể vuông góc với cạnh lòng ở đâu?
Đường trung tuyến vô tam giác cân nặng rất có thể vuông góc với cạnh lòng bên trên đỉnh tam giác.
Để minh chứng điều này, tớ cần dùng một trong những đặc thù của tam giác cân nặng.
1. Đường trung tuyến vô tam giác cân nặng là đoạn trực tiếp nối kể từ đỉnh tam giác cho tới trung điểm của cạnh lòng.
2. Tam giác cân nặng đem nhị cạnh đều nhau và nhị góc đỉnh đều nhau.
3. Đường trung tuyến kể từ đỉnh tam giác là lối trung trực của cạnh lòng.
Giả sử tớ đem tam giác cân nặng ABC, với AB = AC và những góc A, B, C.
Đường trung tuyến vô tam giác cân nặng là đoạn trực tiếp AD, nối kể từ đỉnh A cho tới trung điểm D của cạnh BC.
Chúng tớ cần thiết minh chứng rằng AD vuông góc với BC.
Theo đặc thù 3, AD là lối trung trực của cạnh BC, tức là AD phân chia BC trở nên nhị phần đều nhau.
Ta đã và đang hiểu được tam giác cân nặng đem nhị cạnh đều nhau, nên tớ đem BD = DC.
Do tê liệt, tớ đem tứ giác ABCD là tứ giác cân nặng, với BD = DC và AD là lối trung trực của BC.
Tinđắk xứng cơ bạn dạng cho thấy rằng vô tứ giác cân nặng, lối trung trực của một cạnh vuông góc với cạnh đối lập.
Áp dụng đặc thù này vô tứ giác ABCD, tớ đem lối trung tuyến AD vuông góc với cạnh BC bên trên trung điểm D.
Vậy, tớ tiếp tục minh chứng được rằng vô tam giác cân nặng, lối trung tuyến rất có thể vuông góc với cạnh lòng bên trên đỉnh tam giác.
_HOOK_
Cách vẽ đường trung tuyến trong tam giác cân?
Cách vẽ đường trung tuyến trong tam giác cân như sau:
Bước 1: Vẽ một tam giác cân nặng với nhị cạnh lòng đều nhau và nhị góc đỉnh cũng đều nhau.
Bước 2: Chọn một đỉnh ngẫu nhiên của tam giác thực hiện đỉnh A.
Bước 3: Vẽ một quãng trực tiếp kể từ đỉnh A cho tới trung điểm của cạnh đối lập được gọi là trung điểm của cạnh BC. Đây đó là lối trung tuyến cần thiết lần.
Bước 4: Đến trên đây, các bạn tiếp tục hoàn thiện việc vẽ đường trung tuyến trong tam giác cân.
Đường trung tuyến vô tam giác cân nặng là đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh đối lập. Đường trung tuyến này còn có đặc thù là vuông góc với cạnh lòng và hạn chế cạnh lòng trở nên nhị phần đều nhau.
Hy vọng phản hồi này hữu ích cho tới bạn!
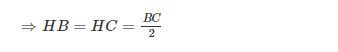
Tầm cần thiết của đường trung tuyến trong tam giác cân?
Đường trung tuyến vô tam giác cân nặng đem vai trò quan trọng đặc biệt trong những việc hiểu và giải quyết và xử lý những yếu tố tương quan cho tới tam giác cân nặng. Dưới đấy là những vai trò của đường trung tuyến trong tam giác cân:
1. Phân phân chia tam giác: Đường trung tuyến phân chia tam giác cân nặng trở nên nhị tam giác cân nặng nhỏ đem diện tích S đều nhau. Như vậy giúp chúng ta làm rõ rộng lớn về tỷ trọng và đối sánh của những thành phần vô tam giác.
2. Đường trung tuyến và lối cao nằm trong gốc bên trên điểm trung điểm: Trong tam giác cân nặng, lối trung tuyến từ là một đỉnh đó là lối cao kể từ đỉnh đối lập. Như vậy tạo nên một góc vuông thân thuộc lối trung tuyến và lối cao bên trên điểm trung điểm. Như vậy xúc tiến việc mày mò và làm rõ rộng lớn về côn trùng tương tác trong số những thành phần của tam giác.
3. Đường trung tuyến là lối trực kí thác với cạnh đáy: Đường trung tuyến vô tam giác cân nặng kể từ góc đỉnh là lối trực kí thác với cạnh lòng ứng. Như vậy xác định quan hệ hình học tập trong số những đoạn trực tiếp vô tam giác và cung ứng vấn đề cần thiết về góc và tỷ trọng vô tam giác cân nặng.
4. Quy tắc điểm trung điểm: Đường trung tuyến vô tam giác cân nặng hạn chế nhau bên trên một điểm độc nhất, gọi là vấn đề trung điểm. Điểm này còn có tầm quan trọng cần thiết trong những việc mày mò những đặc thù và quy tắc của tam giác cân nặng, là vấn đề kí thác của lối cao và lối trực quan.
Tóm lại, đường trung tuyến trong tam giác cân không chỉ có đem sự đối sánh quan trọng đặc biệt với những thành phần không giống vô tam giác mà còn phải đưa đến những vấn đề hình học tập cần thiết. Hiểu rõ ràng vai trò này sẽ hỗ trợ tớ vận dụng và dùng lối trung tuyến một cơ hội hiệu suất cao trong những việc giải quyết và xử lý những câu hỏi tương quan cho tới tam giác cân nặng.
Đường trung tuyến của tam giác | Toán 7 | OLM.VN
OLM.VN: Truy cập OLM.VN nhằm mày mò tức thì những đoạn phim hữu ích và thú vị về toán học tập. Từ những bài xích giảng cụ thể cho tới những phân tách thâm thúy, OLM.VN đem lại cho chính mình một thưởng thức học hành tuyệt hảo. Đừng bỏ qua thời cơ nâng cấp kỹ năng của bạn!
Đường trung tuyến vô tam giác cân nặng đem phần mềm vô cuộc sống thực không?
Đường trung tuyến vô tam giác cân nặng được tạo nên bằng phương pháp nối đỉnh của tam giác với điểm trung điểm của cạnh đối lập. Vì tam giác cân nặng đem những cạnh đối xứng, lối trung tuyến tiếp tục là một trong đoạn trực tiếp trải qua trọng tâm của tam giác và hạn chế cạnh lòng trở nên nhị phần đều nhau.
Trong cuộc sống thực, đường trung tuyến trong tam giác cân đem một trong những phần mềm cần thiết. Dưới đấy là một trong những ví dụ về phần mềm của đường trung tuyến trong tam giác cân:
1. Trong con kiến trúc: Đường trung tuyến vô tam giác cân nặng rất có thể được dùng nhằm kiến thiết phong cách thiết kế, nhất là trong những việc xác lập trọng tâm của một cấu tạo. Trọng tâm của một cấu tạo là một trong điểm cần thiết nhằm đáp ứng tính ổn định ấn định và thăng bằng của cấu tạo.
2. Trong giáo dục: Đường trung tuyến vô tam giác cân nặng được dùng nhằm giảng dạy dỗ và học hành về hình học tập tam giác và những đặc thù của chính nó. Việc hiểu và phần mềm đường trung tuyến trong tam giác cân chung học viên cải tiến và phát triển kỹ năng suy nghĩ hình học tập và logic.
3. Trong xác định và đo đạc: Đường trung tuyến vô tam giác cân nặng cũng rất có thể được dùng trong các việc xác định và đo lường. Ví dụ, vô việc làm đo lường địa hình, người tớ rất có thể dùng lối trung tuyến nhằm xác xác định trí trung tâm của một điểm.
4. Trong thực hành: Đường trung tuyến vô tam giác cân nặng cũng rất có thể được vận dụng trong không ít nghành nghề dịch vụ thực tiễn không giống nhau, ví dụ như kiến thiết, chuyên môn, design thành phầm, v.v. Tại những nghành nghề dịch vụ này, việc hiểu và phần mềm đường trung tuyến trong tam giác cân rất có thể chung nâng cấp hiệu suất thao tác và tăng tính đúng mực của việc làm.
Tóm lại, đường trung tuyến trong tam giác cân đem thật nhiều phần mềm vô cuộc sống thực, kể từ phong cách thiết kế cho tới dạy dỗ và thực hành thực tế. Việc hiểu và vận dụng đường trung tuyến trong tam giác cân rất có thể đưa đến nhiều quyền lợi cho tới việc giải quyết và xử lý những yếu tố thực tiễn và cải tiến và phát triển kỹ năng suy nghĩ hình học tập.
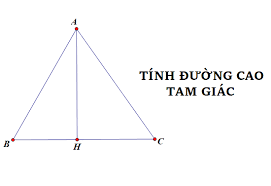
Làm thế nào là nhằm minh chứng rằng đường trung tuyến trong tam giác cân là lối trung trực của cạnh đáy?
Để minh chứng rằng đường trung tuyến trong tam giác cân là lối trung trực của cạnh lòng, tất cả chúng ta cần dùng những đặc thù của tam giác cân nặng và tổ chức thực hiện công việc sau đây:
Bước 1: Giả sử tớ đem tam giác ABC là một trong tam giác cân nặng với những cạnh AB = AC.
Bước 2: Vẽ lối trung tuyến AM kể từ đỉnh A xuống trung điểm M của cạnh BC.
Bước 3: Chúng tớ cần thiết minh chứng rằng lối trung tuyến AM là lối trung trực của cạnh BC, hoặc rằng cách thứ hai, AM vuông góc với BC.
Bước 4: Vì tam giác ABC là tam giác cân nặng, nên tớ đem AB = AC.
Bước 5: Vì M là trung điểm của BC, nên tớ đem BM = CM.
Bước 6: Khi tớ phối kết hợp những fake thiết AB = AC và BM = CM, tớ đã đạt được AM hạn chế BC trở nên nhị phần đều nhau.
Bước 7: Do AM hạn chế BC trở nên nhị phần đều nhau, nên tớ đem AM = MC và AM = MB.
Bước 8: Ta tiếp tục đem AM = MC và AM = MB. Khi nhị đoạn trực tiếp có tính nhiều năm đều nhau, tất cả chúng ta rất có thể Kết luận rằng lối trung tuyến AM vuông góc với BC.
Bước 9: Như vậy, tất cả chúng ta minh chứng thành công xuất sắc rằng đường trung tuyến trong tam giác cân là lối trung trực của cạnh lòng.
Chú ý: Ngoài việc dùng những đặc thù của tam giác cân nặng, tất cả chúng ta cũng rất có thể dùng đặc thù của đường thẳng liền mạch trung trực nhằm minh chứng rằng đường trung tuyến trong tam giác cân là lối trung trực của cạnh lòng.
Xem thêm: chúc sinh nhật em trai
Có từng nào phương pháp để tính diện tích S những tam giác nhỏ rộng lớn được tạo nên vì chưng những lối trung tuyến của tam giác cân?
Có tổng số 6 phương pháp để tính diện tích S những tam giác nhỏ rộng lớn được tạo nên vì chưng những lối trung tuyến của tam giác cân nặng.
Bước 1: Xác ấn định những lối trung tuyến của tam giác cân nặng. Một tam giác cân nặng đem hai tuyến đường trung tuyến, này đó là những đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh lòng ứng.
Bước 2: Tính phỏng nhiều năm những lối trung tuyến. Để tính phỏng nhiều năm của một lối trung tuyến vô tam giác, tớ rất có thể dùng công thức: phỏng nhiều năm lối trung tuyến = (1/2) x phỏng nhiều năm cạnh lòng.
Bước 3: Tính diện tích S của những tam giác nhỏ. cũng có thể dùng công thức diện tích S tam giác: diện tích S tam giác = (1/2) x lối cao x lòng tam giác.
Bước 4: Tính toán diện tích S từng tam giác nhỏ bằng phương pháp vận dụng công thức diện tích S tam giác với lối cao là phỏng nhiều năm của lối trung tuyến và lòng tam giác là phỏng nhiều năm cạnh lòng.
Bước 5: Tổng thích hợp diện tích S những tam giác nhỏ. Cộng tổng diện tích S của những tam giác nhỏ lại cùng nhau.
Qua quy trình đo lường và tính toán, tớ sẽ sở hữu được được tổng số 6 diện tích S những tam giác nhỏ rộng lớn được tạo nên vì chưng những lối trung tuyến của tam giác cân nặng.
_HOOK_
TOÁN 7 - ĐƯỜNG TRUNG TUYẾN TRONG TAM GIÁC - CHỨNG MINH GIAO 3 ĐƯỜNG TRUNG TUYẾN BẰNG CÁCH XẾP GIẤY
Đường trung tuyến là một trong định nghĩa cần thiết vô tam giác, và đoạn phim này tiếp tục phân tích và lý giải một cơ hội cụ thể và dễ nắm bắt về lối trung tuyến. Hãy coi đoạn phim nhằm làm rõ rộng lớn về đặc thù và phần mềm của lối trung tuyến vô tam giác.











Bình luận