Chủ đề diện tích S hình trụ: Diện tích hình trụ là 1 trong định nghĩa cần thiết trong nghề hình học tập. Đây là diện tích S toàn cỗ không khí cướp lưu giữ bởi vì hình trụ, bao hàm diện tích S xung xung quanh và diện tích S nhì lòng. Diện tích hình trụ hoàn toàn có thể được xem toán đơn giản và dễ dàng trải qua những công thức như 2πr(r+h) hoặc 2πrh. Việc đo lường diện tích S hình trụ không chỉ có chung tất cả chúng ta nắm rõ rộng lớn về dáng vẻ của chính nó, mà còn phải hoàn toàn có thể vận dụng vô nhiều việc thực tiễn không giống nhau.
Diện tích hình trụ là gì?
Diện tích hình trụ là tổng diện tích S xung xung quanh và diện tích S nhì lòng của hình trụ. Để tính diện tích toàn phần của hình trụ, tao đem công việc sau:
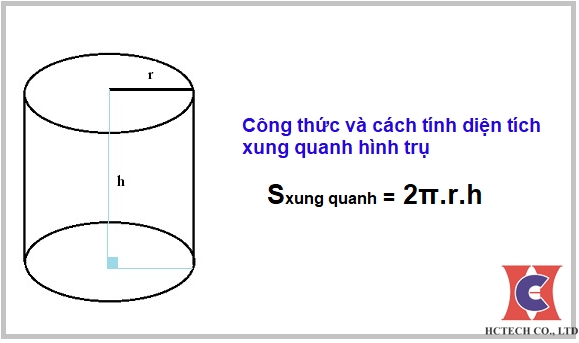
1. Tính diện tích S xung xung quanh (Sxq) của hình trụ: Sxq = 2πrh, vô tê liệt r là nửa đường kính lòng của hình trụ và h là độ cao của hình trụ. Đây là diện tích S của phần thân thích của hình trụ.
2. Tính diện tích S nhì lòng (Sđ) của hình trụ: Sđ = πr^2, vô tê liệt r là nửa đường kính lòng của hình trụ. Đây là diện tích S của nhì mặt mũi lòng của hình trụ.
3. Tính diện tích S toàn phần (Stp) của hình trụ: Stp = Sxq + 2Sđ. Đây là tổng diện tích S xung xung quanh và diện tích S nhì lòng của hình trụ.
Với những độ quý hiếm nửa đường kính lòng và độ cao của hình trụ vẫn cho tới, tao hoàn toàn có thể vận dụng công thức bên trên nhằm tính được diện tích toàn phần của hình trụ.
Bạn đang xem: diện tích toàn phần của hình trụ
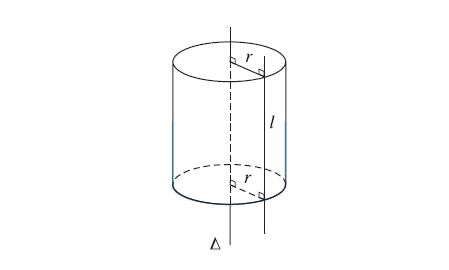

Diện tích xung xung quanh của hình trụ được xem như vậy nào?
Để tính diện tích S xung xung quanh của hình trụ, tao người sử dụng công thức Sxq = 2πrh, vô tê liệt r là nửa đường kính lòng của hình trụ và h là độ cao của hình trụ. Thứ nhất, tao nhân nửa đường kính lòng của hình trụ với độ cao, tiếp sau đó nhân sản phẩm với hằng số pi (π), ở đầu cuối nhân sản phẩm phiên tê liệt với 2. Kết ngược nhận được đó là diện tích S xung xung quanh của hình trụ.
Diện tích nhì lòng của hình trụ được xem như vậy nào?
Để tính diện tích S nhì lòng của hình trụ, tao nên biết được diện tích S lòng của hình trụ. Diện tích lòng của hình trụ được xem bởi vì công thức diện tích S của hình trụ, tức là S = π * r^2, với r là nửa đường kính lòng của hình trụ. Sau tê liệt, tao nhân diện tích S lòng này cho tới 2 nhằm tính được diện tích S nhì lòng của hình trụ. Do tê liệt, công thức nhằm tính diện tích S nhì lòng của hình trụ là S = 2 * π * r^2.
Công thức tính diện tích toàn phần của hình trụ là gì?
Công thức tính diện tích toàn phần của hình trụ là: S = 2πr(r + h).
Trong đó:
- S là diện tích toàn phần của hình trụ.
- π là số Pi, xấp xỉ khoảng chừng 3.14.
- r là nửa đường kính lòng của hình trụ.
- h là độ cao của hình trụ.
Cách tính diện tích toàn phần của hình trụ bởi vì công thức bên trên là nhân nửa đường kính với tổng của nó và độ cao, tiếp sau đó nhân sản phẩm với 2 và số Pi nhằm tính được diện tích S toàn phần.
Làm thế này nhằm tính diện tích toàn phần của hình trụ đem nửa đường kính và độ cao vẫn biết?
Để tính diện tích toàn phần của hình trụ, tao dùng công thức S = 2πrh + 2πr^2, với r là nửa đường kính và h là độ cao của hình trụ vẫn biết.
Bước 1: Tính diện tích S xung xung quanh của hình trụ bởi vì công thức Sxq = 2πrh. Với r là nửa đường kính và h là độ cao vẫn biết.
Bước 2: Tính diện tích S nhì lòng của hình trụ bởi vì công thức Sđ = πr^2, với r là nửa đường kính vẫn biết.
Bước 3: Tính tổng nhì diện tích S bên trên để sở hữu được diện tích toàn phần của hình trụ, bởi vì công thức S = Sxq + Sđ.
Ví dụ: Giả sử nửa đường kính (r) của hình trụ là 6 centimet và độ cao (h) là 8 centimet.
Bước 1: Tính diện tích S xung xung quanh của hình trụ. Sxq = 2πrh = 2π(6)(8) = 96π cm^2.
Bước 2: Tính diện tích S nhì lòng của hình trụ. Sđ = πr^2 = π(6^2) = 36π cm^2.
Bước 3: Tính tổng nhì diện tích S bên trên để sở hữu được diện tích toàn phần của hình trụ. S = Sxq + Sđ = 96π + 36π = 132π cm^2.
Vậy diện tích toàn phần của hình trụ vô ví dụ này là khoảng chừng 132π cm^2, tức khoảng chừng 414.8 cm^2 (kết ngược đã thử tròn).

_HOOK_
Hình trụ, Diện tích xung xung quanh và thể tích của hình trụ - Bài 1 - Toán học tập 9
Bạn mong muốn mày mò về thể tích hình trụ? Video này tiếp tục chỉ dẫn các bạn phương pháp tính và vận dụng thể tích hình trụ trong số việc thực tiễn. Không nên bỏ lỡ thời cơ học hỏi và giao lưu có lợi này!
Tính thể tích hình trụ - Tính diện tích S lòng hình trụ là hình trụ - Tính độ cao của hình trụ π=3,14
Đang học tập toán lớp 9 và bắt gặp khó khăn khăn? Video này tiếp tục giúp cho bạn nắm rõ rộng lớn những định nghĩa và cách thức giải toán toán học tập lớp
Để tính diện tích S toàn phần hình trụ, nên biết những thông số kỹ thuật nào?
Để tính diện tích S toàn phần của một hình trụ, nên biết những thông số kỹ thuật sau:
1. Bán kính lòng r: Đây là phỏng nhiều năm kể từ tâm lòng hình trụ cho tới ngẫu nhiên điểm này bên trên đàng viền lòng.
2. Chiều cao h: Đây là độ cao kể từ lòng hình trụ lên tới đỉnh của chính nó.
Sau Lúc đem những thông số kỹ thuật bên trên, tao triển khai công việc sau nhằm tính diện tích toàn phần của hình trụ:
1. Tính diện tích S xung xung quanh hình trụ: Diện tích xung xung quanh (Sxq) của hình trụ đem công thức là Sxq = 2πr * h, vô tê liệt π là số pi (khoảng 3.14), r là nửa đường kính lòng, và h là độ cao hình trụ.
2. Tính diện tích S nhì đáy: Diện tích lòng bên dưới (Sđ) và diện tích S lòng bên trên (Sđ\') được xem bởi vì công thức Sđ = πr^2, vô tê liệt r là nửa đường kính lòng.
3. Tính diện tích S toàn phần: Diện tích toàn phần (S) của hình trụ là tổng của diện tích S xung xung quanh và diện tích S nhì lòng. Công thức tính là S = Sxq + Sđ + Sđ\'.
Ví dụ: Nếu nửa đường kính lòng r = 6 centimet và độ cao h = 8 centimet, liệu rằng diện tích toàn phần của hình trụ là bao nhiêu?
1. Tính diện tích S xung quanh: Sxq = 2πr * h = 2 * 3.14 * 6 * 8 = 301.44 cm^2.
2. Tính diện tích S nhì đáy: Sđ = Sđ\' = πr^2 = 3.14 * 6^2 = 113.04 cm^2.
3. Tính diện tích S toàn phần: S = Sxq + Sđ + Sđ\' = 301.44 + 113.04 + 113.04 = 527.52 cm^2.
Vậy diện tích toàn phần của hình trụ là khoảng chừng 527.52 cm^2.
Diện tích toàn phần hình trụ đem tương quan gì cho tới diện tích S xung xung quanh và diện tích S nhì đáy?
Diện tích toàn phần của một hình trụ đem tương quan cho tới diện tích S xung xung quanh và diện tích S nhì lòng. Để tính diện tích S toàn phần hình trụ, tao cần thiết tính tổng của diện tích S xung xung quanh và diện tích S nhì lòng.
- Diện tích xung xung quanh hình trụ được xem bởi vì công thức: Sxq = 2 * π * r * h, vô tê liệt r là nửa đường kính lòng của hình trụ, h là độ cao của hình trụ.
- Diện tích nhì lòng của hình trụ được xem bởi vì công thức: Sđáy = π * r^2, vô tê liệt r là nửa đường kính lòng của hình trụ.
Tổng nằm trong nhì diện tích S này đó là diện tích toàn phần của hình trụ: Stp = Sxq + 2 * Sđáy.
Ví dụ, nếu như mang trong mình 1 hình trụ đem nửa đường kính lòng r = 6cm và độ cao h = 8cm, tao hoàn toàn có thể tính diện tích S toàn phần như sau:
- Tính diện tích S xung quanh: Sxq = 2 * π * 6 * 8 ≈ 301.6cm^2.
- Tính diện tích S nhì đáy: Sđáy = π * (6^2) = 113.1cm^2.
Thay vô công thức tổng diện tích S toàn phần: Stp = 301.6 + 2 * 113.1 ≈ 527cm^2.
Do tê liệt, diện tích toàn phần của hình trụ bên trên là khoảng chừng 527cm^2.
Xem thêm: tạo biệt danh theo tên
Cách tính diện tích S xung xung quanh của một hình trụ tròn?
Để tính diện tích S xung xung quanh của một hình trụ tròn trặn, tao dùng công thức Sxq = 2πrh. Trong số đó, π (pi) là một vài xấp xỉ bởi vì 3.14, r là nửa đường kính lòng của hình trụ, và h là độ cao của hình trụ.
Bước 1: Xác toan nửa đường kính r và độ cao h của hình trụ.
Bước 2: Sử dụng công thức Sxq = 2πrh nhằm tính diện tích S xung xung quanh. Thay độ quý hiếm của r và h vô công thức.
Bước 3: Tính toán sản phẩm.
VD: Giả sử nửa đường kính r của hình trụ là 5 centimet và độ cao h là 7 centimet.
Sxq = 2πrh = 2 * 3.14 * 5 * 7 = 219.8 cm2.
Đây đó là diện tích S xung xung quanh của hình trụ tròn trặn đem nửa đường kính 5 centimet và độ cao 7 centimet.
Toán học tập lớp 9 - Chương 4 - Bài 1 - Diện tích xung xung quanh và thể tích hình trụ - Tiết 1
Đừng bỏ qua thời cơ nâng lên kỹ năng toán của bạn!
Diện tích xung xung quanh của hình trụ được xem ra sao lúc biết nửa đường kính và chiều cao?
Để tính diện tích S xung xung quanh của hình trụ, tao dùng công thức: Sxq = 2πrh, vô tê liệt r là nửa đường kính của lòng hình trụ, và h là độ cao của hình trụ.
Bước 1: Xác toan nửa đường kính r và độ cao h của hình trụ.
Bước 2: Sử dụng công thức Sxq = 2πrh nhằm tính diện tích S xung xung quanh của hình trụ bằng phương pháp thay cho độ quý hiếm nửa đường kính r và độ cao h vô công thức.
Ví dụ: Nếu nửa đường kính r = 6 centimet và độ cao h = 8 centimet, tao thay cho vô công thức Sxq = 2πrh nhằm tính diện tích S xung xung quanh của hình trụ:
Sxq = 2π * 6 * 8 = 96π = khoảng chừng 301.6 cm^2.
Vì vậy, diện tích S xung xung quanh của hình trụ là khoảng chừng 301.6 cm^2 lúc biết nửa đường kính và độ cao của hình trụ là 6 centimet và 8 centimet ứng.

Công thức tính diện tích S toàn phần hình trụ Lúc tuy nhiên nửa đường kính và độ cao vẫn biết?
Công thức tính diện tích S toàn phần của một hình trụ lúc biết nửa đường kính (r) và độ cao (h) là:
Diện tích xung quanh: Sxq = 2πrh
Diện tích nhì đáy: Sđ = πr^2
Diện tích toàn phần của hình trụ: S = Sxq + 2Sđ
= 2πrh + 2πr^2
= 2πr(h+r)
Ví dụ: Nếu nửa đường kính của hình trụ là 6 centimet và độ cao là 8 centimet, tao có:
S = 2π(6)(8+6)
= 2π(6)(14)
= 2π(84)
≈ 527 cm²
Do tê liệt, diện tích toàn phần của hình trụ là khoảng chừng 527 cm².
_HOOK_
Tại sao diện tích S toàn phần hình trụ được xem bởi vì tổng diện tích S xung xung quanh và diện tích S nhì đáy?
Diện tích toàn phần của một hình trụ được xem bởi vì tổng của diện tích S xung xung quanh và diện tích S nhì lòng của hình trụ. Vấn đề này hoàn toàn có thể được phân tích và lý giải bởi vì công thức như sau:
Diện tích xung xung quanh của hình trụ được xem bởi vì công thức Sxq = 2πrh, vô tê liệt r là nửa đường kính lòng của hình trụ và h là độ cao của hình trụ. Đây là diện tích S của toàn cỗ mặt phẳng xung xung quanh hình trụ.
Diện tích nhì lòng của hình trụ được xem bởi vì công thức Sđ = πr^2, vô tê liệt r là nửa đường kính của lòng hình trụ. Đây là diện tích S của nhì lòng của hình trụ, ứng với diện tích S của nhì hình trụ.
Tổng diện tích S xung xung quanh và diện tích S nhì lòng tiếp tục cho tới tao diện tích toàn phần của hình trụ, như sau:
Stp = Sxq + Sđ = 2πrh + πr^2.
Vì vậy, diện tích toàn phần của hình trụ được xem bởi vì tổng diện tích S xung xung quanh và diện tích S nhì lòng và được trình diễn bởi vì công thức Stp = 2πrh + πr^2.
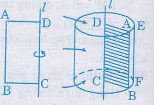
Hình trụ - diện tích S xung xung quanh và thể tích hình trụ - Toán 9 - Thầy Trần Trung Hải
Muốn hiểu biết thêm về thầy Trần Trung Hải - một nghề giáo toán học tập tài ba? Video này tiếp tục reviews về cuộc sống thường ngày và cách thức giảng dạy dỗ rất dị của thầy Trần Trung Hải. Đừng nhằm cách thức giảng dạy dỗ rất dị này qua loa mắt!
Diện tích toàn phần hình trụ hoàn toàn có thể dùng làm tính những gì?
Diện tích toàn phần hình trụ hoàn toàn có thể dùng làm tính diện tích S xung xung quanh và diện tích S nhì lòng của hình trụ. Diện tích xung xung quanh của hình trụ được xem bởi vì công thức Sxq = 2πrh, vô tê liệt r là nửa đường kính lòng hình trụ, h là độ cao hình trụ. Diện tích nhì lòng của hình trụ được xem bởi vì công thức Sđ = πr^2. Tổng nằm trong diện tích S xung xung quanh và diện tích S nhì lòng sẽ tạo nên trở thành diện tích S toàn phần hình trụ. Việc tính diện tích S toàn phần hình trụ chung tất cả chúng ta nắm rõ rộng lớn về hình dạng và cướp lưu giữ không khí của hình trụ.
Làm sao tính diện tích S xung xung quanh của một hình trụ không tồn tại chiều cao?
Để tính diện tích S xung xung quanh của một hình trụ không tồn tại độ cao, tao nên biết nửa đường kính của hình trụ. Diện tích xung xung quanh của hình trụ không tồn tại độ cao (SXQ) được xem bởi vì công thức SXQ = 2πrh, vô tê liệt r là nửa đường kính của lòng hình trụ và h là độ cao của chính nó. Tuy nhiên, với hình trụ không tồn tại độ cao (h = 0), công thức này phát triển thành SXQ = 2πrh = 2πr * 0 = 0. Do tê liệt, diện tích S xung xung quanh của một hình trụ không tồn tại độ cao là 0.
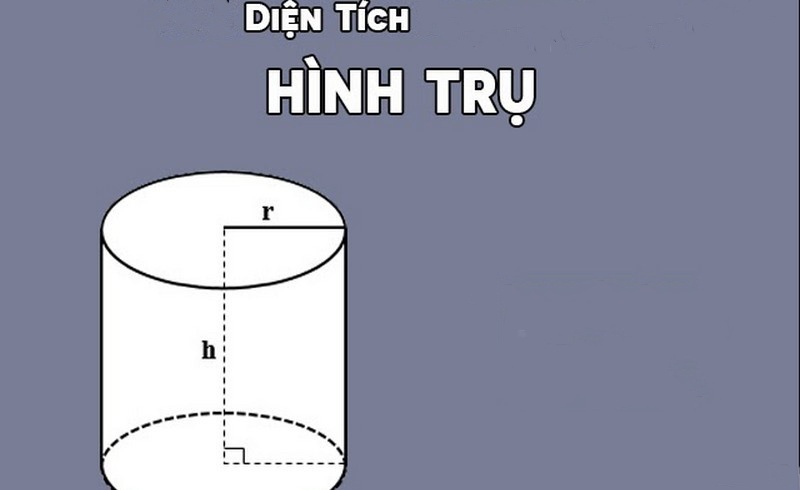
Bước tính diện tích S của hình trụ đem gì không giống đối với bước tính diện tích S hình hộp?
Bước tính diện tích S của hình trụ không giống đối với bước tính diện tích S hình vỏ hộp cũng chính vì hình trụ đem cấu tạo không giống nhau. Để tính diện tích S của hình trụ, tất cả chúng ta cần thiết tính diện tích S xung xung quanh và diện tích S nhì lòng của chính nó.
Bước 1: Tính diện tích S xung xung quanh (Sxq) của hình trụ theo gót công thức Sxq = 2πrh, vô tê liệt r là nửa đường kính của lòng và h là độ cao của hình trụ.
Bước 2: Tính diện tích S nhì lòng (Sđ) của hình trụ theo gót công thức Sđ = πr^2.
Bước 3: Tính diện tích S toàn phần (Stp) của hình trụ bằng phương pháp nằm trong tổng diện tích S xung xung quanh và diện tích S nhì đáy: Stp = Sxq + Sđ.
Ví dụ: Giả sử nửa đường kính của lòng hình trụ là 6 centimet và độ cao là 8 centimet.
Bước 1: Tính diện tích S xung xung quanh = 2πrh = 2π(6)(8) = 96π cm^2.
Bước 2: Tính diện tích S nhì lòng = πr^2 = π(6)^2 = 36π cm^2.
Bước 3: Tính diện tích S toàn phần = Sxq + Sđ = 96π + 36π = 132π cm^2.
Vậy, diện tích toàn phần của hình trụ vô ví dụ này là khoảng chừng 132π cm^2.
Xem thêm: cách nhận biết cô be khít
Có cơ hội này không giống nhằm tính diện tích S toàn phần hình trụ không?
Có rất nhiều cách thức không giống nhau nhằm tính diện tích S toàn phần của một hình trụ. Dưới đó là 1 trong các số những phương pháp:
Bước 1: Xác toan độ cao của hình trụ (h) và nửa đường kính của lòng (r).
Bước 2: Tính diện tích S của lòng hình trụ bởi vì công thức Sđ = π * r^2.
Bước 3: Tính diện tích S xung xung quanh hình trụ bởi vì công thức Sxq = 2 * π * r * h.
Bước 4: Tính diện tích toàn phần của hình trụ bởi vì tổng diện tích S xung xung quanh và diện tích S đáy: STP = Sxq + 2 * Sđ.
Ví dụ: Giả sử độ cao của hình trụ là 8 centimet và nửa đường kính của lòng là 6 centimet.
Bước 1: h = 8 centimet, r = 6 centimet.
Bước 2: Sđ = π * 6^2 = 36π cm^2.
Bước 3: Sxq = 2 * π * 6 * 8 = 96π cm^2.
Bước 4: STP = Sxq + 2 * Sđ = 96π + 2 * 36π = 96π + 72π = 168π cm^2.
Vậy, diện tích toàn phần của hình trụ là 168π cm^2.
_HOOK_










Bình luận