công thức tam giác vuông

Hệ thức lượng vô tam giác vuông là kỹ năng cơ phiên bản quan trọng mang đến học viên lớp 9. Để giải bài bác tập luyện một cơ hội nhanh nhất có thể và hiểu yếu tố thì bạn phải nắm rõ những công thức được công ty chúng tôi tổ hợp tức thì tiếp sau đây.

Bạn đang xem: công thức tam giác vuông

1. Các hệ thức lượng giác vô tam giác vuông

1.1 Hệ thức tương quan về cạnh và đàng cao

Trong đề bài bác tao sở hữu một hình tam giác vuông ABC và tài liệu được mang đến sẵn là vuông bên trên A cùng theo với AH là đàng cao của tam giác này, khi cơ tao sở hữu những hệ thức tuy nhiên chúng ta học viên lớp 9 lưu ý tương quan sau đây:

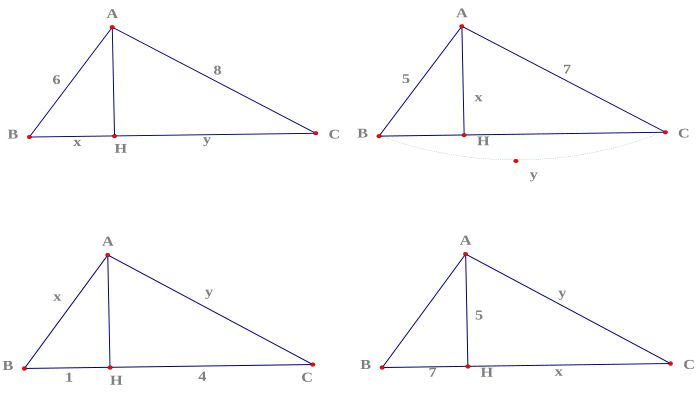
Các hệ thức tương quan cho tới hệ thức lượng vô tam giác vuông và tam giác thường 

• AB bình = BH * BC
• AC bình = CH * BC
• AH bình = BH * CH
• AB * AC = AH * BC
• 1/đường cao bình = 1/AB bình * 1/AC bình
• Cạnh huyền vô tam giác bình phương vị tổng bình phương của nhì cạnh góc vuông vô tam giác cơ.

1.2 Tỉ con số giác của góc nhọn

Một số kỹ năng cần thiết sở hữu tương quan cho tới những công thức lượng giác và hệ thức lượng tam giác vuông tuy nhiên công ty chúng tôi sẵn sàng nhắc cho tới như sau:

a) Định nghĩa về tỉ con số giác

• Sin alpha = Đối / Huyền
• Cos alpha = Kề / Huyền
• Tan alpha = Đối / Kề
• Cot alpha = Kề / Đối

b) Định lý về tỷ con số giác

Trong một tam giác vuông được mang đến sẵn , nếu như nhì góc phụ nhau thì sở hữu công thức vận dụng giải bài bác tập luyện như: sin góc này vị cos góc cơ, tan góc này vị cot góc cơ và ngược lại.

c) Các đối chiếu lưu ý của hệ con số giác

Cho 2 góc alpha và belta được trao diện là 2 góc nhọn của một tam giác vuông tức là nhì góc sở hữu tổng số đo là 90 phỏng và alpha nhỏ hơn belta thì:

• Sin alpha < Sin beta và mặt khác Tan alpha < Tan beta
• Cos alpha > Cos beta và tương tự động tao sở hữu Cot alpha > Cot beta
• Sin alpha < Tan alpha và ngoài ra thì Cos alpha < Cot alpha

2. 4 Định lý lượng giác vô tam giác vuông

Các tấp tểnh lý lượng giác vô tam giác vuông được công ty chúng tôi tổ hợp nhằm chúng ta học tập dinh cơ dễ dàng học tập và dễ dàng tưởng tượng hơn:

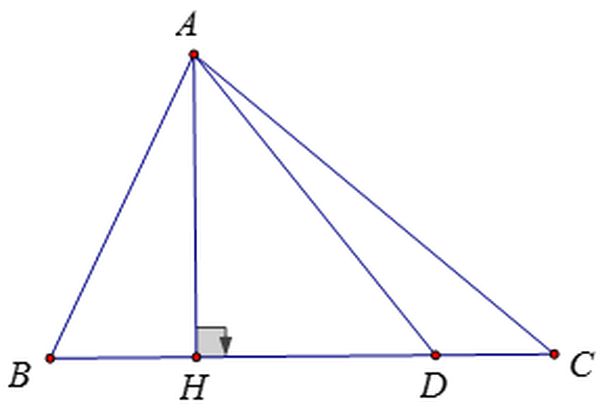
Định lí 1

Trong một tam giác vuông bất kì, tao luôn luôn sở hữu bình phương từng cạnh góc vuông vị tích của cạnh huyền vô tam giác cơ và hình chiếu ứng của cạnh góc vuông cơ ứng với cạnh huyền.

b² = ab’ ; c² = ac’

Định lí 2

Trong một tam giác vuông bất kì, bình phương đàng cao ứng với cạnh huyền tiếp tục vị tích nhì hình chiếu của nhì cạnh góc vuông ứng cơ bên trên cạnh huyền.

h² = b’c’

Định lí 3

Trong một tam giác vuông mang đến sẵn, tích nhì cạnh góc vuông vị tích của cạnh huyền ứng và đàng cao nối kể từ đỉnh góc vuông của tam giác cơ.

ah = bc

Xem thêm: sắp đến tháng thử que có lên 2 vạch không

Định lí 4

Trong một tam giác vuông được mang đến sẵn, nghịch tặc hòn đảo của bình phương đàng cao ứng với cạnh huyền vô tam giác này sẽ vị tổng những nghịch tặc hòn đảo của bình phương nhì cạnh góc vuông ứng.

3. Tỉ con số giác của góc nhọn

Nếu α mang đến trước là 1 góc nhọn ngẫu nhiên thì:

• 0 < sinα <1
• 0< cosα <1, tanα > 0
• cotα > 0, sin2α + cos2α = 1
• tanα.cotα = 1; tanα = sinα.cosα
• cotα = cosα.sinα
• 1 + tan2α = 1cos2α
• 1 + cot2α = 1sin2α

4. Hướng dẫn một trong những dạng bài bác tập luyện hệ thức lượng vô tam giác

Dưới đó là một trong những dạng bài bác tập luyện vượt trội thay mặt đại diện mang đến việc vận dụng những hệ thức lượng vô tam giác vuông lớp 9 được nêu đi ra ở trên:

4.1 Chứng minh những hệ thức và tính độ quý hiếm của biểu thức 

Phương pháp giải:

Vận dụng những cách thức chứng tỏ đẳng thức: chuyển đổi nhằm nhì vế đều bằng nhau, kể từ fake thiết thuở đầu dẫn theo đẳng thức đang được thừa nhận là trúng,… Vận dụng những tấp tểnh lý vô tam giác vuông, tam giác thông thường, những hệ thức lượng giác.

4.2 Tính toán những đại lượng

Phương pháp giải:

Vận dụng tính sin, cos, trung tuyến, diện tích S và côn trùng contact trong số những đại lượng cần thiết tính, những tam giác đặc trưng.

4.3 Chứng minh tam giác 

Phương pháp giải:

Vận dụng những hệ thức lượng giác, tấp tểnh lý, công thức diện tích S, đàng trung tuyến, những bất phương trình và hằng số cơ phiên bản.

4.4 Các vấn đề thực tiễn về giải tam giác

Phương pháp giải cụ thể:

Giải tam giác là lần số đo những cạnh và góc sót lại vô tam giác lúc biết fake thiết, áp dụng những hệ thức lượng, tấp tểnh lý, công thức diện tích S, đàng trung tuyến,... Bài toán thực tiễn giải được. bằng phương pháp xoay quay về vấn đề tam giác nhằm xác lập số đo cần thiết thiết

5. Tổng ăn ý bài bác tập luyện áp dụng và chỉ dẫn giải cụ thể nhất

Bài 1: Cho tam giác vuông ABC vuông bên trên A, sở hữu đàng cao AH của tam giác vuông phân chia cạnh huyền trở nên nhì đoạn trực tiếp có tính nhiều năm theo thứ tự là 3 và 4. Vận dụng những mối quan hệ đang được học tập ở chỗ bên trên nhằm rất có thể tính những cạnh. góc vuông của tam giác ABC như hình minh hoạ bên trên.

Lời giải: Ở vấn đề này trước tiên tao cần thiết xét những nguyên tố dữ khiếu nại tuy nhiên vấn đề đang được mang đến. Lưu ý những góc vuông ứng và xác lập đâu là cạnh huyền và góc này là góc vuông. Sau cơ để ý những cạnh cần thiết tính là nằm trong cạnh này của tam giác vuông. Sau cơ, đánh giá những tài liệu có trước và lựa chọn thông số ứng nhằm vận dụng. Đối với vấn đề này tao dùng hệ thức thân thiện cạnh góc vuông và hình chiếu nhằm đo lường và tính toán theo đòi đòi hỏi của vấn đề.

Bài tập luyện 2: Cho tam giác ABC vuông bên trên A sở hữu cạnh góc vuông kề với góc 60 phỏng của tam giác vuông này vị 3. Sử dụng bảng lượng giác những góc đặc trưng nhằm lần cạnh huyền và cạnh góc vuông sót lại (Lưu ý bạn phải thực hiện tròn xoe số vừa phải tính cho tới chữ số thập phân loại tư nhé).

Giải: Một tam giác ABC vuông cân nặng bên trên A thì vô 2 góc sót lại, góc to hơn là 60 phỏng và ngược lại là 30 phỏng. Khi cơ cạnh đối lập của góc 60 phỏng cơ vị 3. Sau cơ tao vận dụng từng công thức đang được học tập vô bảng lượng giác nhằm tính cạnh huyền và cạnh góc vuông sót lại.

Xem thêm: happy birthday to me là gì

Bài 3: Vận dụng con kiến ​​thức đang được học tập viết lách những tỉ con số giác sau trở nên những tỉ con số giác của những góc nhỏ rộng lớn 45 phỏng, bao gồm sin 60 phỏng, cos 75 phỏng, sin52 phỏng 30′, cot 82 phỏng, tan 80 phỏng.

Lời giải: Đây là dạng toán cơ phiên bản khi tham gia học về tỉ con số giác của góc nhọn. Trong vấn đề này tao chỉ việc áp dụng tính quality giác của nhì góc đối đỉnh vô một tam giác vuông. Sau cơ thay cho thay đổi nó trở nên độ quý hiếm của góc ứng. 

Trên đó là những vấn đề tổng quan lại được công ty chúng tôi tổ hợp lại về hệ thức lượng vô tam giác vuông và chỉ dẫn một trong những điều giải cụ thể những bài bác tập luyện tương quan. Hy vọng rằng qua chuyện những vấn đề hữu ích bên trên rất có thể giúp cho bạn vô quy trình học tập bài bác và thực hiện bài bác tập luyện nhé.