Căn bậc hai của 3

Bách khoa toàn thư banh Wikipedia

Căn bậc nhị của 3 là một số trong những thực dương sao cho tới khi nhân với chủ yếu nó thì đã cho ra số 3. Chính xác rộng lớn, nó được gọi là căn bậc nhị số học tập của 3, nhằm phân biệt với số tâm sở hữu nằm trong đặc thù. Nó được kí hiệu là √3 hoặc 3^¹⁄₂.

Bạn đang xem: căn bậc 2 của 3

Căn bậc nhị của 3 là một số trong những vô tỉ. Nó còn được biết là hằng số Theodorus, mệnh danh theo gót Theodorus xứ Cyrene, người tiếp tục chứng tỏ tính vô tỉ của chính nó.

Sáu mươi chữ số thứ nhất nhập màn biểu diễn thập phân của chính nó là:

1.73205080756887729352744634150587236694280525381038062805580… (dãy số A002194 nhập bảng OEIS)

Thuật toán tính toán[sửa | sửa mã nguồn]

Có một số trong những phương pháp để xấp xỉ độ quý hiếm của √3. Thuật toán thông thường được sử dụng trong số PC cá thể và PC thu về là cách thức Babylon nhằm tính căn bậc nhị của một số trong những. Các bước tổ chức như sau:

Lấy một số trong những a₀ > 0 bất kì thực hiện độ quý hiếm lúc đầu (càng ngay sát √3 càng tốt)
Tính từng số hạng theo gót công thức truy hồi sau:

Lặp lại bước 2 cho tới khi đạt được phỏng đúng mực quan trọng.

Dãy (a_n) bên trên là mặt hàng quy tụ bậc nhị, tức từng chuyến tính cho tới tao khoảng chừng gấp rất nhiều lần số chữ số thập phân đích thị. Bắt đầu với a₀ = 1 cho tới tao những xấp xỉ:

a₁ = 7/4 = 1.75
a₂ = 97/56 = 1.73214...
a₃ = 18817/10864 = 1.73205081...
a₄ = 708158977/408855776 = 1.732050807568877295...

Tháng 12 năm trước đó, độ quý hiếm của √3 tiếp tục được xem cho tới tối thiểu mươi tỉ chữ số thập phân.^[1]

Xấp xỉ hữu tỉ[sửa | sửa mã nguồn]

Phân số 97/56 (1732142857…) rất có thể được sử dụng thực hiện xấp xỉ cho tới căn bậc nhị của 3. Tuy chỉ mất hình mẫu số 56, nó chỉ cách trở độ quý hiếm đích thị thấp hơn 1/10,000 (khoảng 92×10⁻⁵). Giá trị thực hiện tròn trĩnh 1.732 đích thị cho tới 99.99% độ quý hiếm thực.

Archimedes xác minh rằng (1351/780)²
> 3 > (265/153)²
,^[2] theo lần lượt với sai số là 1/608400 (sáu chữ số thập phân) và 2/23409 (bốn chữ số thập phân).

Liên phân số[sửa | sửa mã nguồn]

√3 rất có thể được màn biểu diễn bởi phân số liên tiếp [1;1,2,1,2,1,2,1,…] (dãy số A040001 nhập bảng OEIS), tức là

Theo đặc thù của liên phân số thì nếu

thì khi n 🡒 ∞

Xem thêm: sắp đến tháng thử que có lên 2 vạch không

Ngoài rời khỏi cũng rất có thể biễu thao diễn bên dưới dạng liên phân số tổng quát mắng như

thực hóa học là [1;1,2,1,2,1,2,1,…] tính nhị số hạng đồng thời.

Biểu thao diễn bình phương[sửa | sửa mã nguồn]

Biểu thức bình phương lồng nhau sau tiến bộ về √3:

Chứng minh tính vô tỉ[sửa | sửa mã nguồn]

Chứng minh bởi lùi vô hạn[sửa | sửa mã nguồn]

Chứng minh thông thường được sử dụng cho tới tính vô tỉ của √3 dùng cách thức lùi vô hạn của Fermat. Phương pháp này rất có thể được vận dụng cho tới bất kì số vẹn toàn này ko nên là số chủ yếu phương.

Giả sử √3 là một số trong những hữu tỉ, tức √3 rất có thể ghi chép bên dưới dạng một phân số tối giản a/b, nhập bại liệt a và b yếu tắc bên nhau.
Ta suy rời khỏi a²/b² = 3 hoặc a² = 3b². (a² và b² là những số nguyên)
Do bại liệt a² phân tách không còn cho tới 3, nên a cũng phân tách không còn cho tới 3, tức tồn bên trên số vẹn toàn k sao cho tới a = 3k.
Thay 3k cho tới a nhập đẳng thức ở bước 2: 3b² = (3k)² tao được b² = 3k².
Lập luận như bước 3, tao được b² là số phân tách không còn cho tới 3, nên b cũng phân tách không còn cho tới 3.
Như vậy cả a và b đều phân tách không còn cho tới 3, nên bọn chúng sở hữu một ước cộng đồng là 3, trái khoáy với fake thiết rằng a và b là nhị số yếu tắc bên nhau.

Chứng minh bởi ấn định lý nghiệm hữu tỉ[sửa | sửa mã nguồn]

Một chứng tỏ không giống cho tới tính vô tỉ của √3 là dùng một tình huống đặc biệt quan trọng của ấn định lý nghiệm hữu tỉ, tuyên bố rằng nếu như P(x) là một trong nhiều thức monic (tức nhiều thức sở hữu thông số bậc tối đa bởi 1) với thông số vẹn toàn, thì bất kì nghiệm hữu tỉ này của P(x) cũng chính là một số trong những vẹn toàn. gí dụng ấn định lý cho tới nhiều thức P(x) = x² − 2, tao suy rời khỏi √3 hoặc là số vẹn toàn hoặc là số vô tỉ. Vì 1 < √3 < 2 nên nó ko là một số trong những vẹn toàn, bởi vậy √3 là một số trong những vô tỉ.

Hình học tập và lượng giác[sửa | sửa mã nguồn]

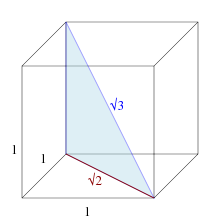
√3 là phỏng lâu năm cạnh của một tam giác đều nội tiếp lối tròn trĩnh sở hữu nửa đường kính bởi 1. Tương tự động, nếu như một tam giác đều phải có cạnh 1 bị chia thành nhị nửa đều nhau, từng nửa là một trong tam giác vuông 30-60-90 với cạnh huyền bởi 1, cạnh góc vuông là 1/2 và √3/2. Từ bại liệt tao suy rời khỏi giá tốt trị những hàm con số giác của 60° và 30°.

Xem thêm: chúc sinh nhật em trai

Căn bậc nhị của 3 cũng xuất hiện tại nhập biểu thức đại số của khá nhiều hằng con số giác như^[3]

Ngoài rời khỏi √3 còn là một khoảng cách thân ái nhị cạnh đối nhau của hình lục giác đều phải có cạnh 1, hoặc là lối chéo cánh của hình lập phương đơn vị chức năng.

Ứng dụng khác[sửa | sửa mã nguồn]

Kỹ thuật điện[sửa | sửa mã nguồn]

Trong năng lượng điện lực, hiệu năng lượng điện thế thân ái nhị chão trộn (điện áp dây) nhập khối hệ thống năng lượng điện phụ vương trộn bởi √3 nhân hiệu năng lượng điện thế của thân ái một chão trộn và chão hòa hợp (điện áp pha). Đây là vì nhị trộn xa nhau chừng 120°, và nhị điểm xa nhau chừng 120 phỏng bên trên lối tròn trĩnh thì sở hữu khoảng cách bởi √3 nhân nửa đường kính lối tròn trĩnh bại liệt.

Xem thêm[sửa | sửa mã nguồn]

Căn bậc nhị của 2
Căn bậc nhị của 5

Ghi chú[sửa | sửa mã nguồn]

Tham khảo[sửa | sửa mã nguồn]

S., D.; Jones, M. F. (1968). “22900D approximations to tướng the square roots of the primes less phàn nàn 100”. Mathematics of Computation. 22 (101): 234–235. doi:10.2307/2004806. JSTOR 2004806.
Uhler, H. S. (1951). “Approximations exceeding 1300 decimals for √3, 1/√3, sin(π/3) and distribution of digits in them”. Proc. Natl. Acad. Sci. U.S.A. 37 (7): 443–447. doi:10.1073/pnas.37.7.443. PMC 1063398. PMID 16578382.
Wells, D. (1997). The Penguin Dictionary of Curious and Interesting Numbers . London: Penguin Group. tr. 23.